1981. Minimize the Difference Between Target and Chosen Elements

Description

You are given an m x n integer matrix mat and an integer target.

Choose one integer from each row in the matrix such that the absolute difference between target and the sum of the chosen elements is minimized.

Return the minimum absolute difference.

The absolute difference between two numbers a and b is the absolute value of a - b.

 

Example 1:

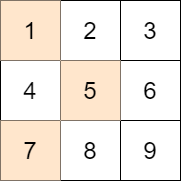
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
Output: 0
Explanation: One possible choice is to:
- Choose 1 from the first row.
- Choose 5 from the second row.
- Choose 7 from the third row.
The sum of the chosen elements is 13, which equals the target, so the absolute difference is 0.

Example 2:

Input: mat = [[1],[2],[3]], target = 100
Output: 94
Explanation: The best possible choice is to:
- Choose 1 from the first row.
- Choose 2 from the second row.
- Choose 3 from the third row.
The sum of the chosen elements is 6, and the absolute difference is 94.

Example 3:

Input: mat = [[1,2,9,8,7]], target = 6
Output: 1
Explanation: The best choice is to choose 7 from the first row.
The absolute difference is 1.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 70
• 1 <= mat[i][j] <= 70
• 1 <= target <= 800

Solutions

Solution 1: Dynamic Programming (Grouped Knapsack)

Let $f[i][j]$ represent whether it is possible to select elements from the first $i$ rows with a sum of $j$. Then we have the state transition equation:

$$ f[i][j] = \begin{cases} 1 & \textit{if there exists } x \in row[i] \textit{ such that } f[i - 1][j - x] = 1 \ 0 & \textit{otherwise} \end{cases} $$

where $row[i]$ represents the set of elements in the $i$-th row.

Since $f[i][j]$ is only related to $f[i - 1][j]$, we can use a rolling array to optimize the space complexity.

Finally, we traverse the $f$ array to find the smallest absolute difference.

The time complexity is $O(m^2 \times n \times C)$ and the space complexity is $O(m \times C)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively, and $C$ is the maximum value of the matrix elements.

Python3JavaJavaC++Go

class Solution:
    def minimizeTheDifference(self, mat: List[List[int]], target: int) -> int:
        f = {0}
        for row in mat:
            f = set(a + b for a in f for b in row)
        return min(abs(v - target) for v in f)

class Solution {
    public int minimizeTheDifference(int[][] mat, int target) {
        boolean[] f = {true};
        for (var row : mat) {
            int mx = 0;
            for (int x : row) {
                mx = Math.max(mx, x);
            }
            boolean[] g = new boolean[f.length + mx];
            for (int x : row) {
                for (int j = x; j < f.length + x; ++j) {
                    g[j] |= f[j - x];
                }
            }
            f = g;
        }
        int ans = 1 << 30;
        for (int j = 0; j < f.length; ++j) {
            if (f[j]) {
                ans = Math.min(ans, Math.abs(j - target));
            }
        }
        return ans;
    }
}

class Solution {
    public int minimizeTheDifference(int[][] mat, int target) {
        Set<Integer> f = new HashSet<>();
        f.add(0);
        for (var row : mat) {
            Set<Integer> g = new HashSet<>();
            for (int a : f) {
                for (int b : row) {
                    g.add(a + b);
                }
            }
            f = g;
        }
        int ans = 1 << 30;
        for (int v : f) {
            ans = Math.min(ans, Math.abs(v - target));
        }
        return ans;
    }
}

class Solution {
public:
    int minimizeTheDifference(vector<vector<int>>& mat, int target) {
        vector<int> f = {1};
        for (auto& row : mat) {
            int mx = *max_element(row.begin(), row.end());
            vector<int> g(f.size() + mx);
            for (int x : row) {
                for (int j = x; j < f.size() + x; ++j) {
                    g[j] |= f[j - x];
                }
            }
            f = move(g);
        }
        int ans = 1 << 30;
        for (int j = 0; j < f.size(); ++j) {
            if (f[j]) {
                ans = min(ans, abs(j - target));
            }
        }
        return ans;
    }
};

func minimizeTheDifference(mat [][]int, target int) int {
    f := []int{1}
    for _, row := range mat {
        mx := slices.Max(row)
        g := make([]int, len(f)+mx)
        for _, x := range row {
            for j := x; j < len(f)+x; j++ {
                g[j] |= f[j-x]
            }
        }
        f = g
    }
    ans := 1 << 30
    for j, v := range f {
        if v == 1 {
            ans = min(ans, abs(j-target))
        }
    }
    return ans
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

Comments