Dynamic Programming
Description
You are given two integers m and n. Consider an m x n grid where each cell is initially white. You can paint each cell red , green , or blue . All cells must be painted.
Return the number of ways to color the grid with no two adjacent cells having the same color . Since the answer can be very large, return it modulo 109 + 7.
Example 1:
Input: m = 1, n = 1
Output: 3
Explanation: The three possible colorings are shown in the image above.
Example 2:
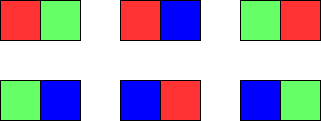
Input: m = 1, n = 2
Output: 6
Explanation: The six possible colorings are shown in the image above.
Example 3:
Input: m = 5, n = 5
Output: 580986
Constraints:
1 <= m <= 51 <= n <= 1000
Solutions
Solution 1: State Compression + Dynamic Programming
We notice that the number of rows in the grid does not exceed \(5\) , so there are at most \(3^5=243\) different color schemes in a column.
Therefore, we define \(f[i][j]\) to represent the number of schemes in the first \(i\) columns, where the coloring state of the \(i\) th column is \(j\) . The state \(f[i][j]\) is transferred from \(f[i - 1][k]\) , where \(k\) is the coloring state of the \(i - 1\) th column, and \(k\) and \(j\) meet the requirement of different colors being adjacent. That is:
\[
f[i][j] = \sum_{k \in \textit{valid}(j)} f[i - 1][k]
\]
where \(\textit{valid}(j)\) represents all legal predecessor states of state \(j\) .
The final answer is the sum of \(f[n][j]\) , where \(j\) is any legal state.
We notice that \(f[i][j]\) is only related to \(f[i - 1][k]\) , so we can use a rolling array to optimize the space complexity.
The time complexity is \(O((m + n) \times 3^{2m})\) , and the space complexity is \(O(3^m)\) . Here, \(m\) and \(n\) are the number of rows and columns of the grid, respectively.
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 class Solution :
def colorTheGrid ( self , m : int , n : int ) -> int :
def f1 ( x : int ) -> bool :
last = - 1
for _ in range ( m ):
if x % 3 == last :
return False
last = x % 3
x //= 3
return True
def f2 ( x : int , y : int ) -> bool :
for _ in range ( m ):
if x % 3 == y % 3 :
return False
x , y = x // 3 , y // 3
return True
mod = 10 ** 9 + 7
mx = 3 ** m
valid = { i for i in range ( mx ) if f1 ( i )}
d = defaultdict ( list )
for x in valid :
for y in valid :
if f2 ( x , y ):
d [ x ] . append ( y )
f = [ int ( i in valid ) for i in range ( mx )]
for _ in range ( n - 1 ):
g = [ 0 ] * mx
for i in valid :
for j in d [ i ]:
g [ i ] = ( g [ i ] + f [ j ]) % mod
f = g
return sum ( f ) % mod
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62 class Solution {
private int m ;
public int colorTheGrid ( int m , int n ) {
this . m = m ;
final int mod = ( int ) 1e9 + 7 ;
int mx = ( int ) Math . pow ( 3 , m );
Set < Integer > valid = new HashSet <> ();
int [] f = new int [ mx ] ;
for ( int i = 0 ; i < mx ; ++ i ) {
if ( f1 ( i )) {
valid . add ( i );
f [ i ] = 1 ;
}
}
Map < Integer , List < Integer >> d = new HashMap <> ();
for ( int i : valid ) {
for ( int j : valid ) {
if ( f2 ( i , j )) {
d . computeIfAbsent ( i , k -> new ArrayList <> ()). add ( j );
}
}
}
for ( int k = 1 ; k < n ; ++ k ) {
int [] g = new int [ mx ] ;
for ( int i : valid ) {
for ( int j : d . getOrDefault ( i , List . of ())) {
g [ i ] = ( g [ i ] + f [ j ] ) % mod ;
}
}
f = g ;
}
int ans = 0 ;
for ( int x : f ) {
ans = ( ans + x ) % mod ;
}
return ans ;
}
private boolean f1 ( int x ) {
int last = - 1 ;
for ( int i = 0 ; i < m ; ++ i ) {
if ( x % 3 == last ) {
return false ;
}
last = x % 3 ;
x /= 3 ;
}
return true ;
}
private boolean f2 ( int x , int y ) {
for ( int i = 0 ; i < m ; ++ i ) {
if ( x % 3 == y % 3 ) {
return false ;
}
x /= 3 ;
y /= 3 ;
}
return true ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59 class Solution {
public :
int colorTheGrid ( int m , int n ) {
auto f1 = [ & ]( int x ) {
int last = -1 ;
for ( int i = 0 ; i < m ; ++ i ) {
if ( x % 3 == last ) {
return false ;
}
last = x % 3 ;
x /= 3 ;
}
return true ;
};
auto f2 = [ & ]( int x , int y ) {
for ( int i = 0 ; i < m ; ++ i ) {
if ( x % 3 == y % 3 ) {
return false ;
}
x /= 3 ;
y /= 3 ;
}
return true ;
};
const int mod = 1e9 + 7 ;
int mx = pow ( 3 , m );
unordered_set < int > valid ;
vector < int > f ( mx );
for ( int i = 0 ; i < mx ; ++ i ) {
if ( f1 ( i )) {
valid . insert ( i );
f [ i ] = 1 ;
}
}
unordered_map < int , vector < int >> d ;
for ( int i : valid ) {
for ( int j : valid ) {
if ( f2 ( i , j )) {
d [ i ]. push_back ( j );
}
}
}
for ( int k = 1 ; k < n ; ++ k ) {
vector < int > g ( mx );
for ( int i : valid ) {
for ( int j : d [ i ]) {
g [ i ] = ( g [ i ] + f [ j ]) % mod ;
}
}
f = move ( g );
}
int ans = 0 ;
for ( int x : f ) {
ans = ( ans + x ) % mod ;
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 func colorTheGrid ( m int , n int ) ( ans int ) {
f1 := func ( x int ) bool {
last := - 1
for i := 0 ; i < m ; i ++ {
if x % 3 == last {
return false
}
last = x % 3
x /= 3
}
return true
}
f2 := func ( x , y int ) bool {
for i := 0 ; i < m ; i ++ {
if x % 3 == y % 3 {
return false
}
x /= 3
y /= 3
}
return true
}
mx := int ( math . Pow ( 3 , float64 ( m )))
valid := map [ int ] bool {}
f := make ([] int , mx )
for i := 0 ; i < mx ; i ++ {
if f1 ( i ) {
valid [ i ] = true
f [ i ] = 1
}
}
d := map [ int ][] int {}
for i := range valid {
for j := range valid {
if f2 ( i , j ) {
d [ i ] = append ( d [ i ], j )
}
}
}
const mod int = 1e9 + 7
for k := 1 ; k < n ; k ++ {
g := make ([] int , mx )
for i := range valid {
for _ , j := range d [ i ] {
g [ i ] = ( g [ i ] + f [ j ]) % mod
}
}
f = g
}
for _ , x := range f {
ans = ( ans + x ) % mod
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 function colorTheGrid ( m : number , n : number ) : number {
const f1 = ( x : number ) : boolean => {
let last = - 1 ;
for ( let i = 0 ; i < m ; ++ i ) {
if ( x % 3 === last ) {
return false ;
}
last = x % 3 ;
x = Math . floor ( x / 3 );
}
return true ;
};
const f2 = ( x : number , y : number ) : boolean => {
for ( let i = 0 ; i < m ; ++ i ) {
if ( x % 3 === y % 3 ) {
return false ;
}
x = Math . floor ( x / 3 );
y = Math . floor ( y / 3 );
}
return true ;
};
const mx = 3 ** m ;
const valid = new Set < number > ();
const f : number [] = Array ( mx ). fill ( 0 );
for ( let i = 0 ; i < mx ; ++ i ) {
if ( f1 ( i )) {
valid . add ( i );
f [ i ] = 1 ;
}
}
const d : Map < number , number [] > = new Map ();
for ( const i of valid ) {
for ( const j of valid ) {
if ( f2 ( i , j )) {
d . set ( i , ( d . get ( i ) || []). concat ( j ));
}
}
}
const mod = 10 ** 9 + 7 ;
for ( let k = 1 ; k < n ; ++ k ) {
const g : number [] = Array ( mx ). fill ( 0 );
for ( const i of valid ) {
for ( const j of d . get ( i ) || []) {
g [ i ] = ( g [ i ] + f [ j ]) % mod ;
}
}
f . splice ( 0 , f . length , ... g );
}
let ans = 0 ;
for ( const x of f ) {
ans = ( ans + x ) % mod ;
}
return ans ;
}
GitHub