Skip to content

1902. Depth of BST Given Insertion Order πŸ”’

Description

You are given a 0-indexed integer array order of length n, a permutation of integers from 1 to n representing the order of insertion into a binary search tree.

A binary search tree is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node's key.
  • The right subtree of a node contains only nodes with keys greater than the node's key.
  • Both the left and right subtrees must also be binary search trees.

The binary search tree is constructed as follows:

  • order[0] will be the root of the binary search tree.
  • All subsequent elements are inserted as the child of any existing node such that the binary search tree properties hold.

Return the depth of the binary search tree.

A binary tree's depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

 

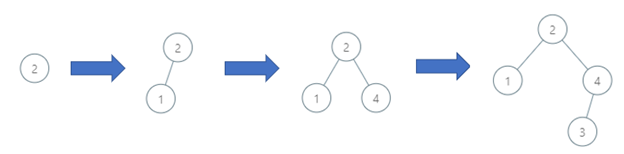
Example 1:

Input: order = [2,1,4,3]
Output: 3
Explanation: The binary search tree has a depth of 3 with path 2->3->4.

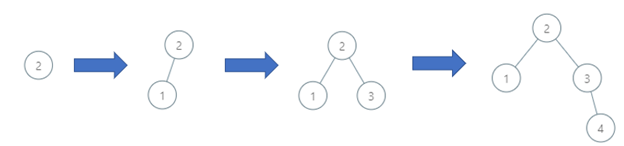
Example 2:

Input: order = [2,1,3,4]
Output: 3
Explanation: The binary search tree has a depth of 3 with path 2->3->4.

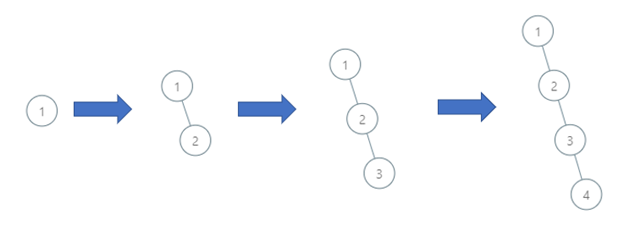
Example 3:

Input: order = [1,2,3,4]
Output: 4
Explanation: The binary search tree has a depth of 4 with path 1->2->3->4.

 

Constraints:

  • n == order.length
  • 1 <= n <= 105
  • order is a permutation of integers between 1 and n.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
from sortedcontainers import SortedDict


class Solution:
    def maxDepthBST(self, order: List[int]) -> int:
        sd = SortedDict({0: 0, inf: 0, order[0]: 1})
        ans = 1
        for v in order[1:]:
            lower = sd.bisect_left(v) - 1
            higher = lower + 1
            depth = 1 + max(sd.values()[lower], sd.values()[higher])
            ans = max(ans, depth)
            sd[v] = depth
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
    public int maxDepthBST(int[] order) {
        TreeMap<Integer, Integer> tm = new TreeMap<>();
        tm.put(0, 0);
        tm.put(Integer.MAX_VALUE, 0);
        tm.put(order[0], 1);
        int ans = 1;
        for (int i = 1; i < order.length; ++i) {
            int v = order[i];
            Map.Entry<Integer, Integer> lower = tm.lowerEntry(v);
            Map.Entry<Integer, Integer> higher = tm.higherEntry(v);
            int depth = 1 + Math.max(lower.getValue(), higher.getValue());
            ans = Math.max(ans, depth);
            tm.put(v, depth);
        }
        return ans;
    }
}

Comments