Array
Matrix
Prefix Sum
Description
A k x k magic square is a k x k grid filled with integers such that every row sum, every column sum, and both diagonal sums are all equal . The integers in the magic square do not have to be distinct . Every 1 x 1 grid is trivially a magic square .
Given an m x n integer grid, return the size (i.e., the side length k) of the largest magic square that can be found within this grid .
Example 1:
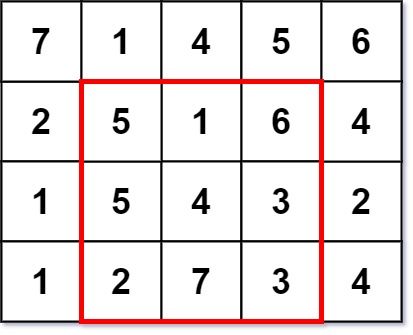
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
Output: 3
Explanation: The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12
Example 2:
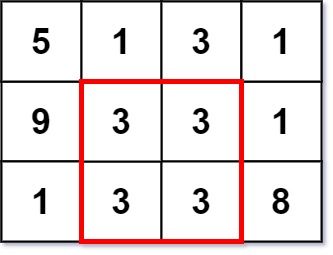
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
Output: 2
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 106
Solutions
Solution 1
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 class Solution :
def largestMagicSquare ( self , grid : List [ List [ int ]]) -> int :
m , n = len ( grid ), len ( grid [ 0 ])
rowsum = [[ 0 ] * ( n + 1 ) for _ in range ( m + 1 )]
colsum = [[ 0 ] * ( n + 1 ) for _ in range ( m + 1 )]
for i in range ( 1 , m + 1 ):
for j in range ( 1 , n + 1 ):
rowsum [ i ][ j ] = rowsum [ i ][ j - 1 ] + grid [ i - 1 ][ j - 1 ]
colsum [ i ][ j ] = colsum [ i - 1 ][ j ] + grid [ i - 1 ][ j - 1 ]
def check ( x1 , y1 , x2 , y2 ):
val = rowsum [ x1 + 1 ][ y2 + 1 ] - rowsum [ x1 + 1 ][ y1 ]
for i in range ( x1 + 1 , x2 + 1 ):
if rowsum [ i + 1 ][ y2 + 1 ] - rowsum [ i + 1 ][ y1 ] != val :
return False
for j in range ( y1 , y2 + 1 ):
if colsum [ x2 + 1 ][ j + 1 ] - colsum [ x1 ][ j + 1 ] != val :
return False
s , i , j = 0 , x1 , y1
while i <= x2 :
s += grid [ i ][ j ]
i += 1
j += 1
if s != val :
return False
s , i , j = 0 , x1 , y2
while i <= x2 :
s += grid [ i ][ j ]
i += 1
j -= 1
if s != val :
return False
return True
for k in range ( min ( m , n ), 1 , - 1 ):
i = 0
while i + k - 1 < m :
j = 0
while j + k - 1 < n :
i2 , j2 = i + k - 1 , j + k - 1
if check ( i , j , i2 , j2 ):
return k
j += 1
i += 1
return 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 class Solution {
private int [][] rowsum ;
private int [][] colsum ;
public int largestMagicSquare ( int [][] grid ) {
int m = grid . length , n = grid [ 0 ] . length ;
rowsum = new int [ m + 1 ][ n + 1 ] ;
colsum = new int [ m + 1 ][ n + 1 ] ;
for ( int i = 1 ; i <= m ; ++ i ) {
for ( int j = 1 ; j <= n ; ++ j ) {
rowsum [ i ][ j ] = rowsum [ i ][ j - 1 ] + grid [ i - 1 ][ j - 1 ] ;
colsum [ i ][ j ] = colsum [ i - 1 ][ j ] + grid [ i - 1 ][ j - 1 ] ;
}
}
for ( int k = Math . min ( m , n ); k > 1 ; -- k ) {
for ( int i = 0 ; i + k - 1 < m ; ++ i ) {
for ( int j = 0 ; j + k - 1 < n ; ++ j ) {
int i2 = i + k - 1 , j2 = j + k - 1 ;
if ( check ( grid , i , j , i2 , j2 )) {
return k ;
}
}
}
}
return 1 ;
}
private boolean check ( int [][] grid , int x1 , int y1 , int x2 , int y2 ) {
int val = rowsum [ x1 + 1 ][ y2 + 1 ] - rowsum [ x1 + 1 ][ y1 ] ;
for ( int i = x1 + 1 ; i <= x2 ; ++ i ) {
if ( rowsum [ i + 1 ][ y2 + 1 ] - rowsum [ i + 1 ][ y1 ] != val ) {
return false ;
}
}
for ( int j = y1 ; j <= y2 ; ++ j ) {
if ( colsum [ x2 + 1 ][ j + 1 ] - colsum [ x1 ][ j + 1 ] != val ) {
return false ;
}
}
int s = 0 ;
for ( int i = x1 , j = y1 ; i <= x2 ; ++ i , ++ j ) {
s += grid [ i ][ j ] ;
}
if ( s != val ) {
return false ;
}
s = 0 ;
for ( int i = x1 , j = y2 ; i <= x2 ; ++ i , -- j ) {
s += grid [ i ][ j ] ;
}
if ( s != val ) {
return false ;
}
return true ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 class Solution {
public :
int largestMagicSquare ( vector < vector < int >>& grid ) {
int m = grid . size (), n = grid . size ();
vector < vector < int >> rowsum ( m + 1 , vector < int > ( n + 1 ));
vector < vector < int >> colsum ( m + 1 , vector < int > ( n + 1 ));
for ( int i = 1 ; i <= m ; ++ i ) {
for ( int j = 1 ; j <= n ; ++ j ) {
rowsum [ i ][ j ] = rowsum [ i ][ j - 1 ] + grid [ i - 1 ][ j - 1 ];
colsum [ i ][ j ] = colsum [ i - 1 ][ j ] + grid [ i - 1 ][ j - 1 ];
}
}
for ( int k = min ( m , n ); k > 1 ; -- k ) {
for ( int i = 0 ; i + k - 1 < m ; ++ i ) {
for ( int j = 0 ; j + k - 1 < n ; ++ j ) {
int i2 = i + k - 1 , j2 = j + k - 1 ;
if ( check ( grid , rowsum , colsum , i , j , i2 , j2 ))
return k ;
}
}
}
return 1 ;
}
bool check ( vector < vector < int >>& grid , vector < vector < int >>& rowsum , vector < vector < int >>& colsum , int x1 , int y1 , int x2 , int y2 ) {
int val = rowsum [ x1 + 1 ][ y2 + 1 ] - rowsum [ x1 + 1 ][ y1 ];
for ( int i = x1 + 1 ; i <= x2 ; ++ i )
if ( rowsum [ i + 1 ][ y2 + 1 ] - rowsum [ i + 1 ][ y1 ] != val )
return false ;
for ( int j = y1 ; j <= y2 ; ++ j )
if ( colsum [ x2 + 1 ][ j + 1 ] - colsum [ x1 ][ j + 1 ] != val )
return false ;
int s = 0 ;
for ( int i = x1 , j = y1 ; i <= x2 ; ++ i , ++ j )
s += grid [ i ][ j ];
if ( s != val )
return false ;
s = 0 ;
for ( int i = x1 , j = y2 ; i <= x2 ; ++ i , -- j )
s += grid [ i ][ j ];
if ( s != val )
return false ;
return true ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 func largestMagicSquare ( grid [][] int ) int {
m , n := len ( grid ), len ( grid [ 0 ])
rowsum := make ([][] int , m + 1 )
colsum := make ([][] int , m + 1 )
for i := 0 ; i <= m ; i ++ {
rowsum [ i ] = make ([] int , n + 1 )
colsum [ i ] = make ([] int , n + 1 )
}
for i := 1 ; i < m + 1 ; i ++ {
for j := 1 ; j < n + 1 ; j ++ {
rowsum [ i ][ j ] = rowsum [ i ][ j - 1 ] + grid [ i - 1 ][ j - 1 ]
colsum [ i ][ j ] = colsum [ i - 1 ][ j ] + grid [ i - 1 ][ j - 1 ]
}
}
for k := min ( m , n ); k > 1 ; k -- {
for i := 0 ; i + k - 1 < m ; i ++ {
for j := 0 ; j + k - 1 < n ; j ++ {
i2 , j2 := i + k - 1 , j + k - 1
if check ( grid , rowsum , colsum , i , j , i2 , j2 ) {
return k
}
}
}
}
return 1
}
func check ( grid , rowsum , colsum [][] int , x1 , y1 , x2 , y2 int ) bool {
val := rowsum [ x1 + 1 ][ y2 + 1 ] - rowsum [ x1 + 1 ][ y1 ]
for i := x1 + 1 ; i < x2 + 1 ; i ++ {
if rowsum [ i + 1 ][ y2 + 1 ] - rowsum [ i + 1 ][ y1 ] != val {
return false
}
}
for j := y1 ; j < y2 + 1 ; j ++ {
if colsum [ x2 + 1 ][ j + 1 ] - colsum [ x1 ][ j + 1 ] != val {
return false
}
}
s := 0
for i , j := x1 , y1 ; i <= x2 ; i , j = i + 1 , j + 1 {
s += grid [ i ][ j ]
}
if s != val {
return false
}
s = 0
for i , j := x1 , y2 ; i <= x2 ; i , j = i + 1 , j - 1 {
s += grid [ i ][ j ]
}
if s != val {
return false
}
return true
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71 function largestMagicSquare ( grid : number [][]) : number {
let m = grid . length ,
n = grid [ 0 ]. length ;
// 前缀和
let rowSum = Array . from ({ length : m + 1 }, ( v , i ) => new Array ( n + 1 ). fill ( 0 )),
colSum = Array . from ({ length : m + 1 }, v => new Array ( n + 1 ). fill ( 0 ));
for ( let i = 0 ; i < m ; i ++ ) {
rowSum [ i + 1 ][ 1 ] = grid [ i ][ 0 ];
for ( let j = 1 ; j < n ; j ++ ) {
rowSum [ i + 1 ][ j + 1 ] = rowSum [ i + 1 ][ j ] + grid [ i ][ j ];
}
}
for ( let j = 0 ; j < n ; j ++ ) {
colSum [ 1 ][ j + 1 ] = grid [ 0 ][ j ];
for ( let i = 1 ; i < m ; i ++ ) {
colSum [ i + 1 ][ j + 1 ] = colSum [ i ][ j + 1 ] + grid [ i ][ j ];
}
}
// console.log(rowSum, colSum)
// 寻找最大k
for ( let k = Math . min ( m , n ); k > 1 ; k -- ) {
for ( let i = 0 ; i + k - 1 < m ; i ++ ) {
for ( let j = 0 ; j + k - 1 < n ; j ++ ) {
let x2 = i + k - 1 ,
y2 = j + k - 1 ;
if ( valid ( grid , rowSum , colSum , i , j , x2 , y2 )) {
return k ;
}
}
}
}
return 1 ;
}
function valid (
grid : number [][],
rowSum : number [][],
colSum : number [][],
x1 : number ,
y1 : number ,
x2 : number ,
y2 : number ,
) : boolean {
let diff = rowSum [ x1 + 1 ][ y2 + 1 ] - rowSum [ x1 + 1 ][ y1 ];
// 行
for ( let i = x1 + 1 ; i <= x2 ; i ++ ) {
if ( diff != rowSum [ i + 1 ][ y2 + 1 ] - rowSum [ i + 1 ][ y1 ]) {
return false ;
}
}
// 列
for ( let j = y1 ; j <= y2 ; j ++ ) {
if ( diff != colSum [ x2 + 1 ][ j + 1 ] - colSum [ x1 ][ j + 1 ]) {
return false ;
}
}
// 主队对角线
let mainSum = diff ;
for ( let i = x1 , j = y1 ; i <= x2 ; i ++ , j ++ ) {
mainSum -= grid [ i ][ j ];
}
if ( mainSum != 0 ) return false ;
// 副对角线
let subSum = diff ;
for ( let i = x1 , j = y2 ; i <= x2 ; i ++ , j -- ) {
subSum -= grid [ i ][ j ];
}
if ( subSum != 0 ) return false ;
return true ;
}