Skip to content

1886. Determine Whether Matrix Can Be Obtained By Rotation

Description

Given two n x n binary matrices mat and target, return true if it is possible to make mat equal to target by rotating mat in 90-degree increments, or false otherwise.

 

Example 1:

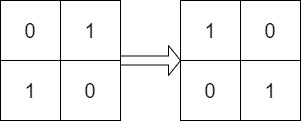
Input: mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise to make mat equal target.

Example 2:

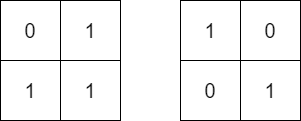
Input: mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
Output: false
Explanation: It is impossible to make mat equal to target by rotating mat.

Example 3:

Input: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise two times to make mat equal target.

 

Constraints:

  • n == mat.length == target.length
  • n == mat[i].length == target[i].length
  • 1 <= n <= 10
  • mat[i][j] and target[i][j] are either 0 or 1.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution:
    def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool:
        def rotate(matrix):
            n = len(matrix)
            for i in range(n // 2):
                for j in range(i, n - 1 - i):
                    t = matrix[i][j]
                    matrix[i][j] = matrix[n - j - 1][i]
                    matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]
                    matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]
                    matrix[j][n - i - 1] = t

        for _ in range(4):
            if mat == target:
                return True
            rotate(mat)
        return False

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public boolean findRotation(int[][] mat, int[][] target) {
        int times = 4;
        while (times-- > 0) {
            if (equals(mat, target)) {
                return true;
            }
            rotate(mat);
        }
        return false;
    }

    private void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; ++i) {
            for (int j = i; j < n - 1 - i; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = t;
            }
        }
    }

    private boolean equals(int[][] nums1, int[][] nums2) {
        int n = nums1.length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (nums1[i][j] != nums2[i][j]) {
                    return false;
                }
            }
        }
        return true;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    bool findRotation(vector<vector<int>>& mat, vector<vector<int>>& target) {
        int n = mat.size();
        for (int k = 0; k < 4; ++k) {
            vector<vector<int>> g(n, vector<int>(n));
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    g[i][j] = mat[j][n - i - 1];
            if (g == target) return true;
            mat = g;
        }
        return false;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func findRotation(mat [][]int, target [][]int) bool {
    n := len(mat)
    for k := 0; k < 4; k++ {
        g := make([][]int, n)
        for i := range g {
            g[i] = make([]int, n)
        }
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                g[i][j] = mat[j][n-i-1]
            }
        }
        if equals(g, target) {
            return true
        }
        mat = g
    }
    return false
}

func equals(a, b [][]int) bool {
    for i, row := range a {
        for j, v := range row {
            if v != b[i][j] {
                return false
            }
        }
    }
    return true
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
function findRotation(mat: number[][], target: number[][]): boolean {
    for (let k = 0; k < 4; k++) {
        rotate(mat);
        if (isEqual(mat, target)) {
            return true;
        }
    }
    return false;
}

function isEqual(A: number[][], B: number[][]) {
    const n = A.length;
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            if (A[i][j] !== B[i][j]) {
                return false;
            }
        }
    }
    return true;
}

function rotate(matrix: number[][]): void {
    const n = matrix.length;
    for (let i = 0; i < n >> 1; i++) {
        for (let j = 0; j < (n + 1) >> 1; j++) {
            [
                matrix[i][j],
                matrix[n - 1 - j][i],
                matrix[n - 1 - i][n - 1 - j],
                matrix[j][n - 1 - i],
            ] = [
                matrix[n - 1 - j][i],
                matrix[n - 1 - i][n - 1 - j],
                matrix[j][n - 1 - i],
                matrix[i][j],
            ];
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
impl Solution {
    pub fn find_rotation(mat: Vec<Vec<i32>>, target: Vec<Vec<i32>>) -> bool {
        let n = mat.len();
        let mut is_equal = [true; 4];
        for i in 0..n {
            for j in 0..n {
                if is_equal[0] && mat[i][j] != target[i][j] {
                    is_equal[0] = false;
                }
                if is_equal[1] && mat[i][j] != target[j][n - 1 - i] {
                    is_equal[1] = false;
                }
                if is_equal[2] && mat[i][j] != target[n - 1 - i][n - 1 - j] {
                    is_equal[2] = false;
                }
                if is_equal[3] && mat[i][j] != target[n - 1 - j][i] {
                    is_equal[3] = false;
                }
            }
        }
        is_equal.into_iter().any(|&v| v)
    }
}

Solution 2

1
2
3
4
5
6
7
class Solution:
    def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool:
        for _ in range(4):
            mat = [list(col) for col in zip(*mat[::-1])]
            if mat == target:
                return True
        return False

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public boolean findRotation(int[][] mat, int[][] target) {
        int n = mat.length;
        for (int k = 0; k < 4; ++k) {
            int[][] g = new int[n][n];
            for (int i = 0; i < n; ++i) {
                for (int j = 0; j < n; ++j) {
                    g[i][j] = mat[j][n - i - 1];
                }
            }
            if (equals(g, target)) {
                return true;
            }
            mat = g;
        }
        return false;
    }

    private boolean equals(int[][] a, int[][] b) {
        int n = a.length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (a[i][j] != b[i][j]) {
                    return false;
                }
            }
        }
        return true;
    }
}

Comments