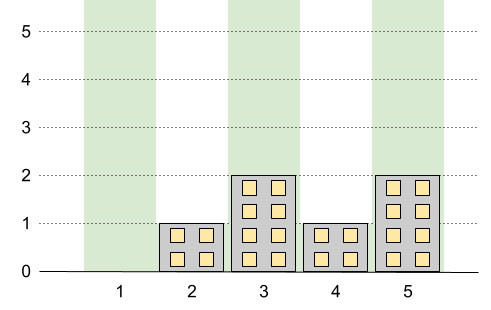Skip to content

1840. Maximum Building Height

Description

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

  • The height of each building must be a non-negative integer.
  • The height of the first building must be 0.
  • The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return the maximum possible height of the tallest building.

 

Example 1:

Input: n = 5, restrictions = [[2,1],[4,1]]
Output: 2
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

Example 2:

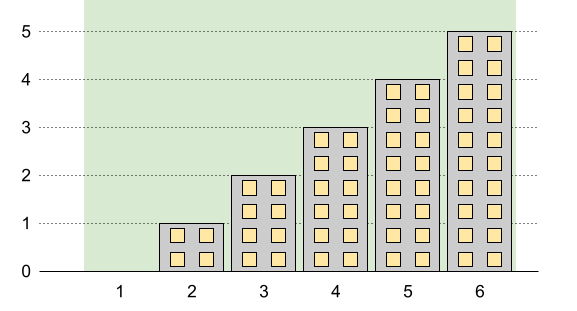
Input: n = 6, restrictions = []
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

Example 3:

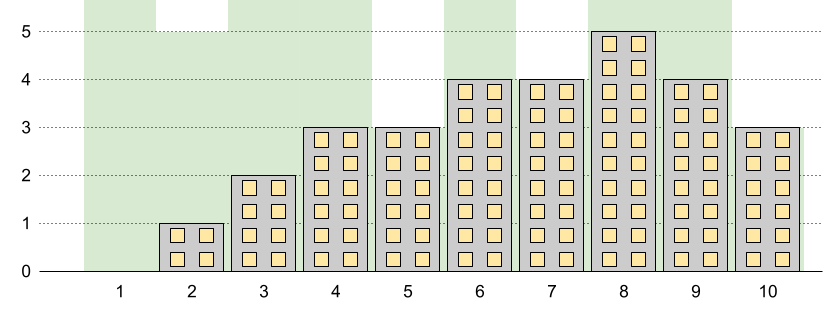
Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

 

Constraints:

  • 2 <= n <= 109
  • 0 <= restrictions.length <= min(n - 1, 105)
  • 2 <= idi <= n
  • idi is unique.
  • 0 <= maxHeighti <= 109

Solutions

Solution 1: Sorting + Mathematics

First, we sort all the constraints by the building number in ascending order.

Then we traverse all the constraints from left to right. For each constraint, we can get an upper bound on the maximum height, i.e., $r_i[1] = \min(r_i[1], r_{i-1}[1] + r_i[0] - r_{i-1}[0])$, where $r_i$ represents the $i$-th constraint, and $r_i[0]$ and $r_i[1]$ represent the building number and the upper bound on the maximum height of the building, respectively.

Next, we traverse all the constraints from right to left. For each constraint, we can get an upper bound on the maximum height, i.e., $r_i[1] = \min(r_i[1], r_{i+1}[1] + r_{i+1}[0] - r_i[0])$.

In this way, we obtain the upper bound on the maximum height for each constrained building.

The problem asks for the height of the tallest building. We can enumerate the buildings between two adjacent constraints $i$ and $i+1$. To maximize the height, the height should first increase and then decrease. Suppose the maximum height is $t$, then $t - r_i[1] + t - r_{i+1}[1] \leq r_{i+1}[0] - r_i[0]$, i.e., $t \leq \frac{r_i[1] + r_{i+1}[1] + r_{i+1}[0] - r_{i}[0]}{2}$. We take the maximum value of all such $t$.

The time complexity is $O(m \times \log m)$, and the space complexity is $O(m)$. Here, $m$ is the number of constraints.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution:
    def maxBuilding(self, n: int, restrictions: List[List[int]]) -> int:
        r = restrictions
        r.append([1, 0])
        r.sort()
        if r[-1][0] != n:
            r.append([n, n - 1])
        m = len(r)
        for i in range(1, m):
            r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0])
        for i in range(m - 2, 0, -1):
            r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0])
        ans = 0
        for i in range(m - 1):
            t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) // 2
            ans = max(ans, t)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int maxBuilding(int n, int[][] restrictions) {
        List<int[]> r = new ArrayList<>();
        r.addAll(Arrays.asList(restrictions));
        r.add(new int[] {1, 0});
        Collections.sort(r, (a, b) -> a[0] - b[0]);
        if (r.get(r.size() - 1)[0] != n) {
            r.add(new int[] {n, n - 1});
        }
        int m = r.size();
        for (int i = 1; i < m; ++i) {
            int[] a = r.get(i - 1), b = r.get(i);
            b[1] = Math.min(b[1], a[1] + b[0] - a[0]);
        }
        for (int i = m - 2; i > 0; --i) {
            int[] a = r.get(i), b = r.get(i + 1);
            a[1] = Math.min(a[1], b[1] + b[0] - a[0]);
        }
        int ans = 0;
        for (int i = 0; i < m - 1; ++i) {
            int[] a = r.get(i), b = r.get(i + 1);
            int t = (a[1] + b[1] + b[0] - a[0]) / 2;
            ans = Math.max(ans, t);
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int maxBuilding(int n, vector<vector<int>>& restrictions) {
        auto&& r = restrictions;
        r.push_back({1, 0});
        ranges::sort(r);
        if (r[r.size() - 1][0] != n) {
            r.push_back({n, n - 1});
        }
        int m = r.size();
        for (int i = 1; i < m; ++i) {
            r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0]);
        }
        for (int i = m - 2; i > 0; --i) {
            r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0]);
        }
        int ans = 0;
        for (int i = 0; i < m - 1; ++i) {
            int t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) / 2;
            ans = max(ans, t);
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
func maxBuilding(n int, restrictions [][]int) (ans int) {
    r := restrictions
    r = append(r, []int{1, 0})
    sort.Slice(r, func(i, j int) bool { return r[i][0] < r[j][0] })
    if r[len(r)-1][0] != n {
        r = append(r, []int{n, n - 1})
    }
    m := len(r)
    for i := 1; i < m; i++ {
        r[i][1] = min(r[i][1], r[i-1][1]+r[i][0]-r[i-1][0])
    }
    for i := m - 2; i > 0; i-- {
        r[i][1] = min(r[i][1], r[i+1][1]+r[i+1][0]-r[i][0])
    }
    for i := 0; i < m-1; i++ {
        t := (r[i][1] + r[i+1][1] + r[i+1][0] - r[i][0]) / 2
        ans = max(ans, t)
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function maxBuilding(n: number, restrictions: number[][]): number {
    restrictions.push([1, 0]);
    restrictions.sort((a, b) => a[0] - b[0]);
    if (restrictions[restrictions.length - 1][0] !== n) {
        restrictions.push([n, n - 1]);
    }

    const m = restrictions.length;
    for (let i = 1; i < m; ++i) {
        restrictions[i][1] = Math.min(
            restrictions[i][1],
            restrictions[i - 1][1] + restrictions[i][0] - restrictions[i - 1][0],
        );
    }

    for (let i = m - 2; i >= 0; --i) {
        restrictions[i][1] = Math.min(
            restrictions[i][1],
            restrictions[i + 1][1] + restrictions[i + 1][0] - restrictions[i][0],
        );
    }

    let ans = 0;
    for (let i = 0; i < m - 1; ++i) {
        const t = Math.floor(
            (restrictions[i][1] +
                restrictions[i + 1][1] +
                restrictions[i + 1][0] -
                restrictions[i][0]) /
                2,
        );
        ans = Math.max(ans, t);
    }

    return ans;
}

Comments