Skip to content

1819. Number of Different Subsequences GCDs

Description

You are given an array nums that consists of positive integers.

The GCD of a sequence of numbers is defined as the greatest integer that divides all the numbers in the sequence evenly.

  • For example, the GCD of the sequence [4,6,16] is 2.

A subsequence of an array is a sequence that can be formed by removing some elements (possibly none) of the array.

  • For example, [2,5,10] is a subsequence of [1,2,1,2,4,1,5,10].

Return the number of different GCDs among all non-empty subsequences of nums.

 

Example 1:

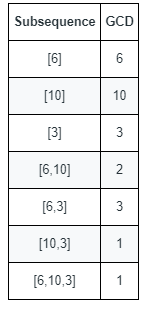
Input: nums = [6,10,3]
Output: 5
Explanation: The figure shows all the non-empty subsequences and their GCDs.
The different GCDs are 6, 10, 3, 2, and 1.

Example 2:

Input: nums = [5,15,40,5,6]
Output: 7

 

Constraints:

  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 2 * 105

Solutions

Solution 1: Enumeration + Mathematics

For all sub-sequences of the array \(nums\), their greatest common divisor (GCD) will not exceed the maximum value \(mx\) in the array.

Therefore, we can enumerate each number \(x\) in \([1,.. mx]\), and determine whether \(x\) is the GCD of a sub-sequence of the array \(nums\). If it is, then we increment the answer by one.

So the problem is transformed into: determining whether \(x\) is the GCD of a sub-sequence of the array \(nums\). We can do this by enumerating the multiples \(y\) of \(x\), and checking whether \(y\) exists in the array \(nums\). If \(y\) exists in the array \(nums\), then we calculate the GCD \(g\) of \(y\). If \(g = x\) occurs, then \(x\) is the GCD of a sub-sequence of the array \(nums\).

The time complexity is \(O(n + M \times \log M)\), and the space complexity is \(O(M)\). Here, \(n\) and \(M\) are the length of the array \(nums\) and the maximum value in the array \(nums\), respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution:
    def countDifferentSubsequenceGCDs(self, nums: List[int]) -> int:
        mx = max(nums)
        vis = set(nums)
        ans = 0
        for x in range(1, mx + 1):
            g = 0
            for y in range(x, mx + 1, x):
                if y in vis:
                    g = gcd(g, y)
                    if g == x:
                        ans += 1
                        break
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int countDifferentSubsequenceGCDs(int[] nums) {
        int mx = Arrays.stream(nums).max().getAsInt();
        boolean[] vis = new boolean[mx + 1];
        for (int x : nums) {
            vis[x] = true;
        }
        int ans = 0;
        for (int x = 1; x <= mx; ++x) {
            int g = 0;
            for (int y = x; y <= mx; y += x) {
                if (vis[y]) {
                    g = gcd(g, y);
                    if (x == g) {
                        ++ans;
                        break;
                    }
                }
            }
        }
        return ans;
    }

    private int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int countDifferentSubsequenceGCDs(vector<int>& nums) {
        int mx = *max_element(nums.begin(), nums.end());
        vector<bool> vis(mx + 1);
        for (int& x : nums) {
            vis[x] = true;
        }
        int ans = 0;
        for (int x = 1; x <= mx; ++x) {
            int g = 0;
            for (int y = x; y <= mx; y += x) {
                if (vis[y]) {
                    g = gcd(g, y);
                    if (g == x) {
                        ++ans;
                        break;
                    }
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func countDifferentSubsequenceGCDs(nums []int) (ans int) {
    mx := slices.Max(nums)
    vis := make([]bool, mx+1)
    for _, x := range nums {
        vis[x] = true
    }
    for x := 1; x <= mx; x++ {
        g := 0
        for y := x; y <= mx; y += x {
            if vis[y] {
                g = gcd(g, y)
                if g == x {
                    ans++
                    break
                }
            }
        }
    }
    return
}

func gcd(a, b int) int {
    if b == 0 {
        return a
    }
    return gcd(b, a%b)
}

Comments