1615. Maximal Network Rank

Description

There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [a_i, b_i] indicates that there is a bidirectional road between cities a_i and b_i.

The network rank of two different cities is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.

The maximal network rank of the infrastructure is the maximum network rank of all pairs of different cities.

Given the integer n and the array roads, return the maximal network rank of the entire infrastructure.

Example 1:

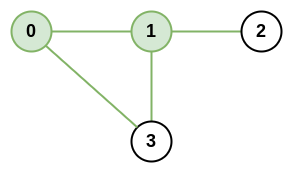
Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
Output: 4
Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.

Example 2:

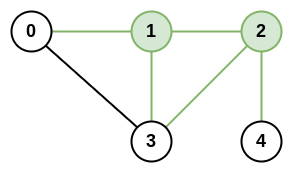
Input: n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
Output: 5
Explanation: There are 5 roads that are connected to cities 1 or 2.

Example 3:

Input: n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
Output: 5
Explanation: The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.

Constraints:

2 <= n <= 100
0 <= roads.length <= n * (n - 1) / 2
roads[i].length == 2
0 <= a_i, b_i <= n-1
a_i != b_i
Each pair of cities has at most one road connecting them.

Solutions

Solution 1: Counting

We can use a one-dimensional array $\textit{cnt}$ to record the degree of each city and a two-dimensional array $\textit{g}$ to record whether there is a road between each pair of cities. If there is a road between city $a$ and city $b$, then $\textit{g}[a][b] = \textit{g}[b][a] = 1$; otherwise, $\textit{g}[a][b] = \textit{g}[b][a] = 0$.

Next, we enumerate each pair of cities $(a, b)$, where $a \lt b$, and calculate their network rank, which is $\textit{cnt}[a] + \textit{cnt}[b] - \textit{g}[a][b]$. The maximum value among these is the answer.

The time complexity is $O(n^2)$, and the space complexity is $O(n^2)$. Here, $n$ is the number of cities.

Python3JavaC++GoTypeScript

class Solution:
    def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
        g = [[0] * n for _ in range(n)]
        cnt = [0] * n
        for a, b in roads:
            g[a][b] = g[b][a] = 1
            cnt[a] += 1
            cnt[b] += 1
        return max(cnt[a] + cnt[b] - g[a][b] for a in range(n) for b in range(a + 1, n))

class Solution {
    public int maximalNetworkRank(int n, int[][] roads) {
        int[][] g = new int[n][n];
        int[] cnt = new int[n];
        for (var r : roads) {
            int a = r[0], b = r[1];
            g[a][b] = 1;
            g[b][a] = 1;
            ++cnt[a];
            ++cnt[b];
        }
        int ans = 0;
        for (int a = 0; a < n; ++a) {
            for (int b = a + 1; b < n; ++b) {
                ans = Math.max(ans, cnt[a] + cnt[b] - g[a][b]);
            }
        }
        return ans;
    }
}

class Solution {
public:
    int maximalNetworkRank(int n, vector<vector<int>>& roads) {
        int cnt[n];
        int g[n][n];
        memset(cnt, 0, sizeof(cnt));
        memset(g, 0, sizeof(g));
        for (auto& r : roads) {
            int a = r[0], b = r[1];
            g[a][b] = g[b][a] = 1;
            ++cnt[a];
            ++cnt[b];
        }
        int ans = 0;
        for (int a = 0; a < n; ++a) {
            for (int b = a + 1; b < n; ++b) {
                ans = max(ans, cnt[a] + cnt[b] - g[a][b]);
            }
        }
        return ans;
    }
};

func maximalNetworkRank(n int, roads [][]int) (ans int) {
    g := make([][]int, n)
    cnt := make([]int, n)
    for i := range g {
        g[i] = make([]int, n)
    }
    for _, r := range roads {
        a, b := r[0], r[1]
        g[a][b], g[b][a] = 1, 1
        cnt[a]++
        cnt[b]++
    }
    for a := 0; a < n; a++ {
        for b := a + 1; b < n; b++ {
            ans = max(ans, cnt[a]+cnt[b]-g[a][b])
        }
    }
    return
}

function maximalNetworkRank(n: number, roads: number[][]): number {
    const g: number[][] = Array.from({ length: n }, () => Array(n).fill(0));
    const cnt: number[] = Array(n).fill(0);
    for (const [a, b] of roads) {
        g[a][b] = 1;
        g[b][a] = 1;
        ++cnt[a];
        ++cnt[b];
    }
    let ans = 0;
    for (let a = 0; a < n; ++a) {
        for (let b = a + 1; b < n; ++b) {
            ans = Math.max(ans, cnt[a] + cnt[b] - g[a][b]);
        }
    }
    return ans;
}

1615. Maximal Network Rank

Description

Solutions

Solution 1: Counting

Comments