1612. Check If Two Expression Trees are Equivalent 🔒

Description

A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (variables), and internal nodes (nodes with two children) correspond to the operators. In this problem, we only consider the '+' operator (i.e. addition).

You are given the roots of two binary expression trees, root1 and root2. Return true if the two binary expression trees are equivalent. Otherwise, return false.

Two binary expression trees are equivalent if they evaluate to the same value regardless of what the variables are set to.

Example 1:

Input: root1 = [x], root2 = [x]
Output: true

Example 2:

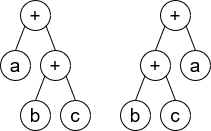
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,c]
Output: true
Explanation: a + (b + c) == (b + c) + a

Example 3:

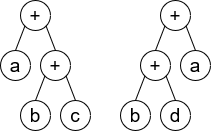
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,d]
Output: false
Explanation: a + (b + c) != (b + d) + a

Constraints:

The number of nodes in both trees are equal, odd and, in the range [1, 4999].
Node.val is '+' or a lower-case English letter.
It's guaranteed that the tree given is a valid binary expression tree.

Follow up: What will you change in your solution if the tree also supports the '-' operator (i.e. subtraction)?

Solutions

Solution 1

Python3JavaC++JavaScript

# Definition for a binary tree node.
# class Node(object):
#     def __init__(self, val=" ", left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool:
        def dfs(root, v):
            if root is None:
                return
            if root.val != '+':
                cnt[root.val] += v
            dfs(root.left, v)
            dfs(root.right, v)

        cnt = Counter()
        dfs(root1, 1)
        dfs(root2, -1)
        return all(x == 0 for x in cnt.values())

/**
 * Definition for a binary tree node.
 * class Node {
 *     char val;
 *     Node left;
 *     Node right;
 *     Node() {this.val = ' ';}
 *     Node(char val) { this.val = val; }
 *     Node(char val, Node left, Node right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int[] cnt = new int[26];

    public boolean checkEquivalence(Node root1, Node root2) {
        dfs(root1, 1);
        dfs(root2, -1);
        for (int x : cnt) {
            if (x != 0) {
                return false;
            }
        }
        return true;
    }

    private void dfs(Node root, int v) {
        if (root == null) {
            return;
        }
        if (root.val != '+') {
            cnt[root.val - 'a'] += v;
        }
        dfs(root.left, v);
        dfs(root.right, v);
    }
}

/**
 * Definition for a binary tree node.
 * struct Node {
 *     char val;
 *     Node *left;
 *     Node *right;
 *     Node() : val(' '), left(nullptr), right(nullptr) {}
 *     Node(char x) : val(x), left(nullptr), right(nullptr) {}
 *     Node(char x, Node *left, Node *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool checkEquivalence(Node* root1, Node* root2) {
        int cnt[26]{};
        function<void(Node*, int)> dfs = [&](Node* root, int v) {
            if (!root) {
                return;
            }
            if (root->val != '+') {
                cnt[root->val - 'a'] += v;
            }
            dfs(root->left, v);
            dfs(root->right, v);
        };
        dfs(root1, 1);
        dfs(root2, -1);
        for (int& x : cnt) {
            if (x) {
                return false;
            }
        }
        return true;
    }
};

/**
 * Definition for a binary tree node.
 * function Node(val, left, right) {
 *     this.val = (val===undefined ? " " : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {Node} root1
 * @param {Node} root2
 * @return {boolean}
 */
var checkEquivalence = function (root1, root2) {
    const cnt = new Array(26).fill(0);
    const dfs = (root, v) => {
        if (!root) {
            return;
        }
        if (root.val !== '+') {
            cnt[root.val.charCodeAt(0) - 'a'.charCodeAt(0)] += v;
        }
        dfs(root.left, v);
        dfs(root.right, v);
    };
    dfs(root1, 1);
    dfs(root2, -1);
    for (const x of cnt) {
        if (x) {
            return false;
        }
    }
    return true;
};

Solution 2