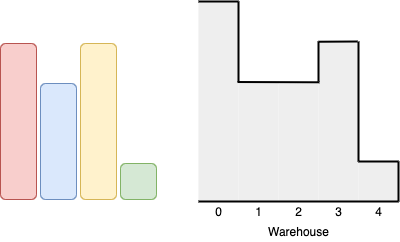1564. Put Boxes Into the Warehouse I 🔒

Description

You are given two arrays of positive integers, boxes and warehouse, representing the heights of some boxes of unit width and the heights of n rooms in a warehouse respectively. The warehouse's rooms are labelled from 0 to n - 1 from left to right where warehouse[i] (0-indexed) is the height of the ith room.

Boxes are put into the warehouse by the following rules:

• Boxes cannot be stacked.
• You can rearrange the insertion order of the boxes.
• Boxes can only be pushed into the warehouse from left to right only.
• If the height of some room in the warehouse is less than the height of a box, then that box and all other boxes behind it will be stopped before that room.

Return the maximum number of boxes you can put into the warehouse.

 

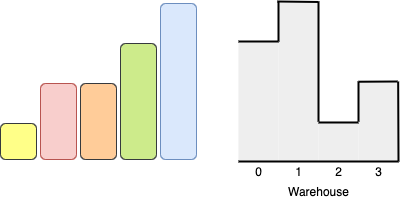
Example 1:

Input: boxes = [4,3,4,1], warehouse = [5,3,3,4,1]
Output: 3
Explanation: 

We can first put the box of height 1 in room 4. Then we can put the box of height 3 in either of the 3 rooms 1, 2, or 3. Lastly, we can put one box of height 4 in room 0.
There is no way we can fit all 4 boxes in the warehouse.

Example 2:

Input: boxes = [1,2,2,3,4], warehouse = [3,4,1,2]
Output: 3
Explanation: 

Notice that it's not possible to put the box of height 4 into the warehouse since it cannot pass the first room of height 3.
Also, for the last two rooms, 2 and 3, only boxes of height 1 can fit.
We can fit 3 boxes maximum as shown above. The yellow box can also be put in room 2 instead.
Swapping the orange and green boxes is also valid, or swapping one of them with the red box.

Example 3:

Input: boxes = [1,2,3], warehouse = [1,2,3,4]
Output: 1
Explanation: Since the first room in the warehouse is of height 1, we can only put boxes of height 1.

 

Constraints:

• n == warehouse.length
• 1 <= boxes.length, warehouse.length <= 105
• 1 <= boxes[i], warehouse[i] <= 109

Solutions

Solution 1

Python3JavaC++GoTypeScript

class Solution:
    def maxBoxesInWarehouse(self, boxes: List[int], warehouse: List[int]) -> int:
        n = len(warehouse)
        left = [warehouse[0]] * n
        for i in range(1, n):
            left[i] = min(left[i - 1], warehouse[i])
        boxes.sort()
        i, j = 0, n - 1
        while i < len(boxes):
            while j >= 0 and left[j] < boxes[i]:
                j -= 1
            if j < 0:
                break
            i, j = i + 1, j - 1
        return i

class Solution {
    public int maxBoxesInWarehouse(int[] boxes, int[] warehouse) {
        int n = warehouse.length;
        int[] left = new int[n];
        left[0] = warehouse[0];
        for (int i = 1; i < n; ++i) {
            left[i] = Math.min(left[i - 1], warehouse[i]);
        }
        Arrays.sort(boxes);
        int i = 0, j = n - 1;
        while (i < boxes.length) {
            while (j >= 0 && left[j] < boxes[i]) {
                --j;
            }
            if (j < 0) {
                break;
            }
            ++i;
            --j;
        }
        return i;
    }
}

class Solution {
public:
    int maxBoxesInWarehouse(vector<int>& boxes, vector<int>& warehouse) {
        int n = warehouse.size();
        int left[n];
        left[0] = warehouse[0];
        for (int i = 1; i < n; ++i) {
            left[i] = min(left[i - 1], warehouse[i]);
        }
        sort(boxes.begin(), boxes.end());
        int i = 0, j = n - 1;
        while (i < boxes.size()) {
            while (j >= 0 && left[j] < boxes[i]) {
                --j;
            }
            if (j < 0) {
                break;
            }
            ++i;
            --j;
        }
        return i;
    }
};

func maxBoxesInWarehouse(boxes []int, warehouse []int) int {
    n := len(warehouse)
    left := make([]int, n)
    left[0] = warehouse[0]
    for i := 1; i < n; i++ {
        left[i] = min(left[i-1], warehouse[i])
    }
    sort.Ints(boxes)
    i, j := 0, n-1
    for i < len(boxes) {
        for j >= 0 && left[j] < boxes[i] {
            j--
        }
        if j < 0 {
            break
        }
        i, j = i+1, j-1
    }
    return i
}

function maxBoxesInWarehouse(boxes: number[], warehouse: number[]): number {
    const n = warehouse.length;
    const left: number[] = new Array(n);
    left[0] = warehouse[0];
    for (let i = 1; i < n; ++i) {
        left[i] = Math.min(left[i - 1], warehouse[i]);
    }
    boxes.sort((a, b) => a - b);
    let i = 0;
    let j = n - 1;
    while (i < boxes.length) {
        while (j >= 0 && left[j] < boxes[i]) {
            --j;
        }
        if (j < 0) {
            break;
        }
        ++i;
        --j;
    }
    return i;
}

Comments