Skip to content

1560. Most Visited Sector in a Circular Track

Description

Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The ith round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]

Return an array of the most visited sectors sorted in ascending order.

Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).

 

Example 1:

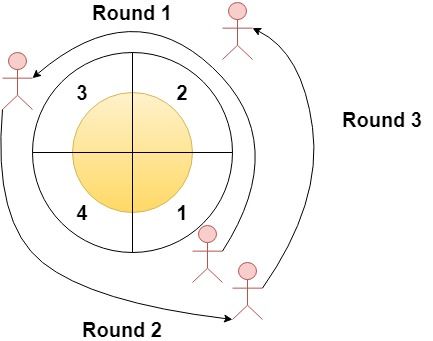
Input: n = 4, rounds = [1,3,1,2]
Output: [1,2]
Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.

Example 2:

Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2]
Output: [2]

Example 3:

Input: n = 7, rounds = [1,3,5,7]
Output: [1,2,3,4,5,6,7]

 

Constraints:

  • 2 <= n <= 100
  • 1 <= m <= 100
  • rounds.length == m + 1
  • 1 <= rounds[i] <= n
  • rounds[i] != rounds[i + 1] for 0 <= i < m

Solutions

Solution 1: Considering the Relationship Between Start and End Positions

Since the end position of each stage is the start position of the next stage, and each stage is in a counterclockwise direction, we can determine the number of times each sector is passed based on the relationship between the start and end positions.

If \(\textit{rounds}[0] \leq \textit{rounds}[m]\), then the sectors from \(\textit{rounds}[0]\) to \(\textit{rounds}[m]\) are passed the most times, and we can directly return all sectors within this interval.

Otherwise, the sectors from \(1\) to \(\textit{rounds}[m]\) and the sectors from \(\textit{rounds}[0]\) to \(n\) form the union of the most passed sectors, and we can return the union of these two intervals.

The time complexity is \(O(n)\), where \(n\) is the number of sectors. Ignoring the space consumption of the answer array, the space complexity is \(O(1)\).

1
2
3
4
5
class Solution:
    def mostVisited(self, n: int, rounds: List[int]) -> List[int]:
        if rounds[0] <= rounds[-1]:
            return list(range(rounds[0], rounds[-1] + 1))
        return list(range(1, rounds[-1] + 1)) + list(range(rounds[0], n + 1))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public List<Integer> mostVisited(int n, int[] rounds) {
        int m = rounds.length - 1;
        List<Integer> ans = new ArrayList<>();
        if (rounds[0] <= rounds[m]) {
            for (int i = rounds[0]; i <= rounds[m]; ++i) {
                ans.add(i);
            }
        } else {
            for (int i = 1; i <= rounds[m]; ++i) {
                ans.add(i);
            }
            for (int i = rounds[0]; i <= n; ++i) {
                ans.add(i);
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> mostVisited(int n, vector<int>& rounds) {
        int m = rounds.size() - 1;
        vector<int> ans;
        if (rounds[0] <= rounds[m]) {
            for (int i = rounds[0]; i <= rounds[m]; ++i) {
                ans.push_back(i);
            }
        } else {
            for (int i = 1; i <= rounds[m]; ++i) {
                ans.push_back(i);
            }
            for (int i = rounds[0]; i <= n; ++i) {
                ans.push_back(i);
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
func mostVisited(n int, rounds []int) []int {
    m := len(rounds) - 1
    var ans []int
    if rounds[0] <= rounds[m] {
        for i := rounds[0]; i <= rounds[m]; i++ {
            ans = append(ans, i)
        }
    } else {
        for i := 1; i <= rounds[m]; i++ {
            ans = append(ans, i)
        }
        for i := rounds[0]; i <= n; i++ {
            ans = append(ans, i)
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
function mostVisited(n: number, rounds: number[]): number[] {
    const ans: number[] = [];
    const m = rounds.length - 1;
    if (rounds[0] <= rounds[m]) {
        for (let i = rounds[0]; i <= rounds[m]; ++i) {
            ans.push(i);
        }
    } else {
        for (let i = 1; i <= rounds[m]; ++i) {
            ans.push(i);
        }
        for (let i = rounds[0]; i <= n; ++i) {
            ans.push(i);
        }
    }
    return ans;
}

Comments