Skip to content

1478. Allocate Mailboxes

Description

Given the array houses where houses[i] is the location of the ith house along a street and an integer k, allocate k mailboxes in the street.

Return the minimum total distance between each house and its nearest mailbox.

The test cases are generated so that the answer fits in a 32-bit integer.

 

Example 1:

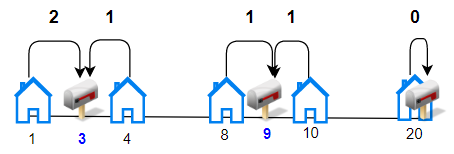
Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5

Example 2:

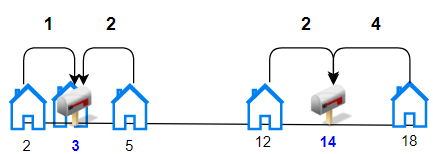
Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

 

Constraints:

  • 1 <= k <= houses.length <= 100
  • 1 <= houses[i] <= 104
  • All the integers of houses are unique.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution:
    def minDistance(self, houses: List[int], k: int) -> int:
        houses.sort()
        n = len(houses)
        g = [[0] * n for _ in range(n)]
        for i in range(n - 2, -1, -1):
            for j in range(i + 1, n):
                g[i][j] = g[i + 1][j - 1] + houses[j] - houses[i]
        f = [[inf] * (k + 1) for _ in range(n)]
        for i in range(n):
            f[i][1] = g[0][i]
            for j in range(2, min(k + 1, i + 2)):
                for p in range(i):
                    f[i][j] = min(f[i][j], f[p][j - 1] + g[p + 1][i])
        return f[-1][k]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int minDistance(int[] houses, int k) {
        Arrays.sort(houses);
        int n = houses.length;
        int[][] g = new int[n][n];
        for (int i = n - 2; i >= 0; --i) {
            for (int j = i + 1; j < n; ++j) {
                g[i][j] = g[i + 1][j - 1] + houses[j] - houses[i];
            }
        }
        int[][] f = new int[n][k + 1];
        final int inf = 1 << 30;
        for (int[] e : f) {
            Arrays.fill(e, inf);
        }
        for (int i = 0; i < n; ++i) {
            f[i][1] = g[0][i];
            for (int j = 2; j <= k && j <= i + 1; ++j) {
                for (int p = 0; p < i; ++p) {
                    f[i][j] = Math.min(f[i][j], f[p][j - 1] + g[p + 1][i]);
                }
            }
        }
        return f[n - 1][k];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int minDistance(vector<int>& houses, int k) {
        int n = houses.size();
        sort(houses.begin(), houses.end());
        int g[n][n];
        memset(g, 0, sizeof(g));
        for (int i = n - 2; ~i; --i) {
            for (int j = i + 1; j < n; ++j) {
                g[i][j] = g[i + 1][j - 1] + houses[j] - houses[i];
            }
        }
        int f[n][k + 1];
        memset(f, 0x3f, sizeof(f));
        for (int i = 0; i < n; ++i) {
            f[i][1] = g[0][i];
            for (int j = 1; j <= k && j <= i + 1; ++j) {
                for (int p = 0; p < i; ++p) {
                    f[i][j] = min(f[i][j], f[p][j - 1] + g[p + 1][i]);
                }
            }
        }
        return f[n - 1][k];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func minDistance(houses []int, k int) int {
    sort.Ints(houses)
    n := len(houses)
    g := make([][]int, n)
    f := make([][]int, n)
    const inf = 1 << 30
    for i := range g {
        g[i] = make([]int, n)
        f[i] = make([]int, k+1)
        for j := range f[i] {
            f[i][j] = inf
        }
    }
    for i := n - 2; i >= 0; i-- {
        for j := i + 1; j < n; j++ {
            g[i][j] = g[i+1][j-1] + houses[j] - houses[i]
        }
    }
    for i := 0; i < n; i++ {
        f[i][1] = g[0][i]
        for j := 2; j <= k && j <= i+1; j++ {
            for p := 0; p < i; p++ {
                f[i][j] = min(f[i][j], f[p][j-1]+g[p+1][i])
            }
        }
    }
    return f[n-1][k]
}

Comments