Skip to content

1424. Diagonal Traverse II

Description

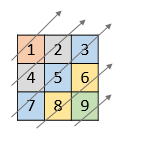
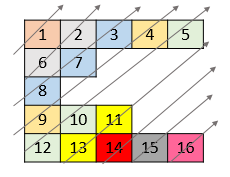
Given a 2D integer array nums, return all elements of nums in diagonal order as shown in the below images.

 

Example 1:

Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

Example 2:

Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

 

Constraints:

  • 1 <= nums.length <= 105
  • 1 <= nums[i].length <= 105
  • 1 <= sum(nums[i].length) <= 105
  • 1 <= nums[i][j] <= 105

Solutions

Solution 1: Sorting

We observe that:

  • The value of $i + j$ is the same for each diagonal;
  • The value of $i + j$ for the next diagonal is greater than that of the previous diagonal;
  • Within the same diagonal, the value of $i + j$ is the same, and the value of $j$ increases from small to large.

Therefore, we store all numbers in the form of $(i, j, \textit{nums}[i][j])$ into $\textit{arr}$, and then sort according to the first two items. Finally, return the array composed of the values at index 2 of all elements in $\textit{arr}$.

The time complexity is $O(n \times \log n)$, where $n$ is the number of elements in the array $\textit{nums}$. The space complexity is $O(n)$.

1
2
3
4
5
6
7
8
class Solution:
    def findDiagonalOrder(self, nums: List[List[int]]) -> List[int]:
        arr = []
        for i, row in enumerate(nums):
            for j, v in enumerate(row):
                arr.append((i + j, j, v))
        arr.sort()
        return [v[2] for v in arr]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public int[] findDiagonalOrder(List<List<Integer>> nums) {
        List<int[]> arr = new ArrayList<>();
        for (int i = 0; i < nums.size(); ++i) {
            for (int j = 0; j < nums.get(i).size(); ++j) {
                arr.add(new int[] {i + j, j, nums.get(i).get(j)});
            }
        }
        arr.sort((a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
        int[] ans = new int[arr.size()];
        for (int i = 0; i < arr.size(); ++i) {
            ans[i] = arr.get(i)[2];
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& nums) {
        vector<tuple<int, int, int>> arr;
        for (int i = 0; i < nums.size(); ++i) {
            for (int j = 0; j < nums[i].size(); ++j) {
                arr.push_back({i + j, j, nums[i][j]});
            }
        }
        sort(arr.begin(), arr.end());
        vector<int> ans;
        for (auto& e : arr) {
            ans.push_back(get<2>(e));
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func findDiagonalOrder(nums [][]int) []int {
    arr := [][]int{}
    for i, row := range nums {
        for j, v := range row {
            arr = append(arr, []int{i + j, j, v})
        }
    }
    sort.Slice(arr, func(i, j int) bool {
        if arr[i][0] == arr[j][0] {
            return arr[i][1] < arr[j][1]
        }
        return arr[i][0] < arr[j][0]
    })
    ans := []int{}
    for _, v := range arr {
        ans = append(ans, v[2])
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function findDiagonalOrder(nums: number[][]): number[] {
    const arr: number[][] = [];
    for (let i = 0; i < nums.length; ++i) {
        for (let j = 0; j < nums[i].length; ++j) {
            arr.push([i + j, j, nums[i][j]]);
        }
    }
    arr.sort((a, b) => (a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]));
    return arr.map(x => x[2]);
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
public class Solution {
    public int[] FindDiagonalOrder(IList<IList<int>> nums) {
        List<int[]> arr = new List<int[]>();
        for (int i = 0; i < nums.Count; ++i) {
            for (int j = 0; j < nums[i].Count; ++j) {
                arr.Add(new int[] { i + j, j, nums[i][j] });
            }
        }
        arr.Sort((a, b) => a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
        int[] ans = new int[arr.Count];
        for (int i = 0; i < arr.Count; ++i) {
            ans[i] = arr[i][2];
        }
        return ans;
    }
}

Comments