1361. Validate Binary Tree Nodes

Description

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

 

Example 1:

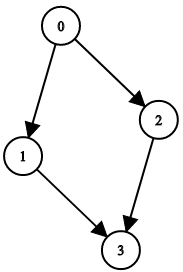
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

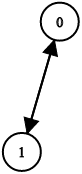
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

 

Constraints:

• n == leftChild.length == rightChild.length
• 1 <= n <= 104
• -1 <= leftChild[i], rightChild[i] <= n - 1

Solutions

Solution 1: Union-Find

We can traverse each node $i$ and its corresponding left and right children $l$, $r$, using an array $vis$ to record whether the node has a parent:

• If the child node already has a parent, it means there are multiple fathers, which does not meet the condition, so we return false directly.
• If the child node and the parent node are already in the same connected component, it means a cycle will be formed, which does not meet the condition, so we return false directly.
• Otherwise, we perform a union operation, set the corresponding position of the $vis$ array to true, and decrease the number of connected components by $1$.

After the traversal, we check whether the number of connected components in the union-find set is $1$. If it is, we return true, otherwise, we return false.

The time complexity is $O(n \times \alpha(n))$, and the space complexity is $O(n)$. Where $n$ is the number of nodes, and $\alpha(n)$ is the inverse Ackermann function, which is less than $5$.

Python3JavaC++Go

class Solution:
    def validateBinaryTreeNodes(
        self, n: int, leftChild: List[int], rightChild: List[int]
    ) -> bool:
        def find(x: int) -> int:
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(n))
        vis = [False] * n
        for i, (a, b) in enumerate(zip(leftChild, rightChild)):
            for j in (a, b):
                if j != -1:
                    if vis[j] or find(i) == find(j):
                        return False
                    p[find(i)] = find(j)
                    vis[j] = True
                    n -= 1
        return n == 1

class Solution {
    private int[] p;

    public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        boolean[] vis = new boolean[n];
        for (int i = 0, m = n; i < m; ++i) {
            for (int j : new int[] {leftChild[i], rightChild[i]}) {
                if (j != -1) {
                    if (vis[j] || find(i) == find(j)) {
                        return false;
                    }
                    p[find(i)] = find(j);
                    vis[j] = true;
                    --n;
                }
            }
        }
        return n == 1;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

class Solution {
public:
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        int p[n];
        iota(p, p + n, 0);
        bool vis[n];
        memset(vis, 0, sizeof(vis));
        function<int(int)> find = [&](int x) {
            return p[x] == x ? x : p[x] = find(p[x]);
        };
        for (int i = 0, m = n; i < m; ++i) {
            for (int j : {leftChild[i], rightChild[i]}) {
                if (j != -1) {
                    if (vis[j] || find(i) == find(j)) {
                        return false;
                    }
                    p[find(i)] = find(j);
                    vis[j] = true;
                    --n;
                }
            }
        }
        return n == 1;
    }
};

func validateBinaryTreeNodes(n int, leftChild []int, rightChild []int) bool {
    p := make([]int, n)
    for i := range p {
        p[i] = i
    }
    var find func(int) int
    find = func(x int) int {
        if p[x] != x {
            p[x] = find(p[x])
        }
        return p[x]
    }
    vis := make([]bool, n)
    for i, a := range leftChild {
        for _, j := range []int{a, rightChild[i]} {
            if j != -1 {
                if vis[j] || find(i) == find(j) {
                    return false
                }
                p[find(i)] = find(j)
                vis[j] = true
                n--
            }
        }
    }
    return n == 1
}

Comments