Dynamic Programming
Graph
Shortest Path
Description
There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi , toi , weighti ] represents a bidirectional and weighted edge between cities fromi and toi , and given the integer distanceThreshold.
Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.
Notice that the distance of a path connecting cities i j
Example 1:
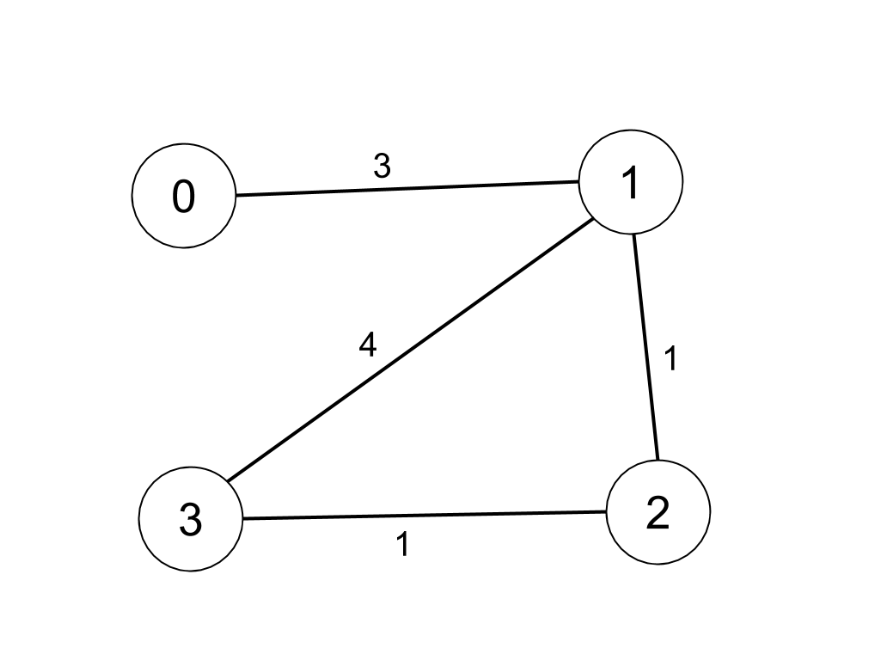
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph.
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2]
City 1 -> [City 0, City 2, City 3]
City 2 -> [City 0, City 1, City 3]
City 3 -> [City 1, City 2]
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
Example 2:
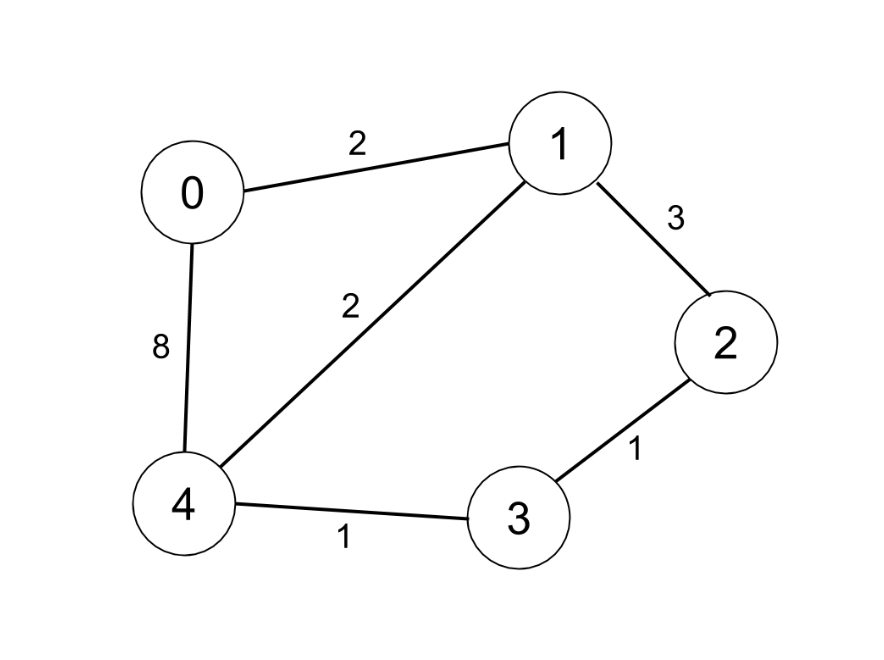
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph.
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1]
City 1 -> [City 0, City 4]
City 2 -> [City 3, City 4]
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3]
The city 0 has 1 neighboring city at a distanceThreshold = 2.
Constraints:
2 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= fromi < toi < n1 <= weighti , distanceThreshold <= 10^4All pairs (fromi , toi ) are distinct.
Solutions
Solution 1
Python3 Java C++ Go TypeScript JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 class Solution :
def findTheCity (
self , n : int , edges : List [ List [ int ]], distanceThreshold : int
) -> int :
def dijkstra ( u : int ) -> int :
dist = [ inf ] * n
dist [ u ] = 0
vis = [ False ] * n
for _ in range ( n ):
k = - 1
for j in range ( n ):
if not vis [ j ] and ( k == - 1 or dist [ k ] > dist [ j ]):
k = j
vis [ k ] = True
for j in range ( n ):
# dist[j] = min(dist[j], dist[k] + g[k][j])
if dist [ k ] + g [ k ][ j ] < dist [ j ]:
dist [ j ] = dist [ k ] + g [ k ][ j ]
return sum ( d <= distanceThreshold for d in dist )
g = [[ inf ] * n for _ in range ( n )]
for f , t , w in edges :
g [ f ][ t ] = g [ t ][ f ] = w
ans , cnt = n , inf
for i in range ( n - 1 , - 1 , - 1 ):
if ( t := dijkstra ( i )) < cnt :
cnt , ans = t , i
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58 class Solution {
private int n ;
private int [][] g ;
private int [] dist ;
private boolean [] vis ;
private final int inf = 1 << 30 ;
private int distanceThreshold ;
public int findTheCity ( int n , int [][] edges , int distanceThreshold ) {
this . n = n ;
this . distanceThreshold = distanceThreshold ;
g = new int [ n ][ n ] ;
dist = new int [ n ] ;
vis = new boolean [ n ] ;
for ( var e : g ) {
Arrays . fill ( e , inf );
}
for ( var e : edges ) {
int f = e [ 0 ] , t = e [ 1 ] , w = e [ 2 ] ;
g [ f ][ t ] = w ;
g [ t ][ f ] = w ;
}
int ans = n , cnt = inf ;
for ( int i = n - 1 ; i >= 0 ; -- i ) {
int t = dijkstra ( i );
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
private int dijkstra ( int u ) {
Arrays . fill ( dist , inf );
Arrays . fill ( vis , false );
dist [ u ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
int k = - 1 ;
for ( int j = 0 ; j < n ; ++ j ) {
if ( ! vis [ j ] && ( k == - 1 || dist [ k ] > dist [ j ] )) {
k = j ;
}
}
vis [ k ] = true ;
for ( int j = 0 ; j < n ; ++ j ) {
dist [ j ] = Math . min ( dist [ j ] , dist [ k ] + g [ k ][ j ] );
}
}
int cnt = 0 ;
for ( int d : dist ) {
if ( d <= distanceThreshold ) {
++ cnt ;
}
}
return cnt ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 class Solution {
public :
int findTheCity ( int n , vector < vector < int >>& edges , int distanceThreshold ) {
int g [ n ][ n ];
int dist [ n ];
bool vis [ n ];
memset ( g , 0x3f , sizeof ( g ));
for ( auto & e : edges ) {
int f = e [ 0 ], t = e [ 1 ], w = e [ 2 ];
g [ f ][ t ] = g [ t ][ f ] = w ;
}
auto dijkstra = [ & ]( int u ) {
memset ( dist , 0x3f , sizeof ( dist ));
memset ( vis , 0 , sizeof ( vis ));
dist [ u ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
int k = -1 ;
for ( int j = 0 ; j < n ; ++ j ) {
if ( ! vis [ j ] && ( k == -1 || dist [ j ] < dist [ k ])) {
k = j ;
}
}
vis [ k ] = true ;
for ( int j = 0 ; j < n ; ++ j ) {
dist [ j ] = min ( dist [ j ], dist [ k ] + g [ k ][ j ]);
}
}
return count_if ( dist , dist + n , [ & ]( int d ) { return d <= distanceThreshold ; });
};
int ans = n , cnt = n + 1 ;
for ( int i = n - 1 ; ~ i ; -- i ) {
int t = dijkstra ( i );
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 func findTheCity ( n int , edges [][] int , distanceThreshold int ) int {
g := make ([][] int , n )
dist := make ([] int , n )
vis := make ([] bool , n )
const inf int = 1e7
for i := range g {
g [ i ] = make ([] int , n )
for j := range g [ i ] {
g [ i ][ j ] = inf
}
}
for _ , e := range edges {
f , t , w := e [ 0 ], e [ 1 ], e [ 2 ]
g [ f ][ t ], g [ t ][ f ] = w , w
}
dijkstra := func ( u int ) ( cnt int ) {
for i := range vis {
vis [ i ] = false
dist [ i ] = inf
}
dist [ u ] = 0
for i := 0 ; i < n ; i ++ {
k := - 1
for j := 0 ; j < n ; j ++ {
if ! vis [ j ] && ( k == - 1 || dist [ j ] < dist [ k ]) {
k = j
}
}
vis [ k ] = true
for j := 0 ; j < n ; j ++ {
dist [ j ] = min ( dist [ j ], dist [ k ] + g [ k ][ j ])
}
}
for _ , d := range dist {
if d <= distanceThreshold {
cnt ++
}
}
return
}
ans , cnt := n , inf
for i := n - 1 ; i >= 0 ; i -- {
if t := dijkstra ( i ); t < cnt {
cnt = t
ans = i
}
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 function findTheCity ( n : number , edges : number [][], distanceThreshold : number ) : number {
const g : number [][] = Array . from ({ length : n }, () => Array ( n ). fill ( Infinity ));
const dist : number [] = Array ( n ). fill ( Infinity );
const vis : boolean [] = Array ( n ). fill ( false );
for ( const [ f , t , w ] of edges ) {
g [ f ][ t ] = g [ t ][ f ] = w ;
}
const dijkstra = ( u : number ) : number => {
dist . fill ( Infinity );
vis . fill ( false );
dist [ u ] = 0 ;
for ( let i = 0 ; i < n ; ++ i ) {
let k = - 1 ;
for ( let j = 0 ; j < n ; ++ j ) {
if ( ! vis [ j ] && ( k === - 1 || dist [ j ] < dist [ k ])) {
k = j ;
}
}
vis [ k ] = true ;
for ( let j = 0 ; j < n ; ++ j ) {
dist [ j ] = Math . min ( dist [ j ], dist [ k ] + g [ k ][ j ]);
}
}
return dist . filter ( d => d <= distanceThreshold ). length ;
};
let ans = n ;
let cnt = Infinity ;
for ( let i = n - 1 ; i >= 0 ; -- i ) {
const t = dijkstra ( i );
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 function findTheCity ( n , edges , distanceThreshold ) {
const g = Array . from ({ length : n }, () => Array ( n ). fill ( Infinity ));
const dist = Array ( n ). fill ( Infinity );
const vis = Array ( n ). fill ( false );
for ( const [ f , t , w ] of edges ) {
g [ f ][ t ] = g [ t ][ f ] = w ;
}
const dijkstra = u => {
dist . fill ( Infinity );
vis . fill ( false );
dist [ u ] = 0 ;
for ( let i = 0 ; i < n ; ++ i ) {
let k = - 1 ;
for ( let j = 0 ; j < n ; ++ j ) {
if ( ! vis [ j ] && ( k === - 1 || dist [ j ] < dist [ k ])) {
k = j ;
}
}
vis [ k ] = true ;
for ( let j = 0 ; j < n ; ++ j ) {
dist [ j ] = Math . min ( dist [ j ], dist [ k ] + g [ k ][ j ]);
}
}
return dist . filter ( d => d <= distanceThreshold ). length ;
};
let ans = n ;
let cnt = Infinity ;
for ( let i = n - 1 ; i >= 0 ; -- i ) {
const t = dijkstra ( i );
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
Solution 2
Python3 Java C++ Go TypeScript JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution :
def findTheCity (
self , n : int , edges : List [ List [ int ]], distanceThreshold : int
) -> int :
g = [[ inf ] * n for _ in range ( n )]
for f , t , w in edges :
g [ f ][ t ] = g [ t ][ f ] = w
for k in range ( n ):
g [ k ][ k ] = 0
for i in range ( n ):
for j in range ( n ):
# g[i][j] = min(g[i][j], g[i][k] + g[k][j])
if g [ i ][ k ] + g [ k ][ j ] < g [ i ][ j ]:
g [ i ][ j ] = g [ i ][ k ] + g [ k ][ j ]
ans , cnt = n , inf
for i in range ( n - 1 , - 1 , - 1 ):
t = sum ( d <= distanceThreshold for d in g [ i ])
if t < cnt :
cnt , ans = t , i
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 class Solution {
public int findTheCity ( int n , int [][] edges , int distanceThreshold ) {
final int inf = 1 << 29 ;
int [][] g = new int [ n ][ n ] ;
for ( var e : g ) {
Arrays . fill ( e , inf );
}
for ( var e : edges ) {
int f = e [ 0 ] , t = e [ 1 ] , w = e [ 2 ] ;
g [ f ][ t ] = w ;
g [ t ][ f ] = w ;
}
for ( int k = 0 ; k < n ; ++ k ) {
g [ k ][ k ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
g [ i ][ j ] = Math . min ( g [ i ][ j ] , g [ i ][ k ] + g [ k ][ j ] );
}
}
}
int ans = n , cnt = inf ;
for ( int i = n - 1 ; i >= 0 ; -- i ) {
int t = 0 ;
for ( int d : g [ i ] ) {
if ( d <= distanceThreshold ) {
++ t ;
}
}
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 class Solution {
public :
int findTheCity ( int n , vector < vector < int >>& edges , int distanceThreshold ) {
int g [ n ][ n ];
memset ( g , 0x3f , sizeof ( g ));
for ( auto & e : edges ) {
int f = e [ 0 ], t = e [ 1 ], w = e [ 2 ];
g [ f ][ t ] = g [ t ][ f ] = w ;
}
for ( int k = 0 ; k < n ; ++ k ) {
g [ k ][ k ] = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
g [ i ][ j ] = min ( g [ i ][ j ], g [ i ][ k ] + g [ k ][ j ]);
}
}
}
int ans = n , cnt = n + 1 ;
for ( int i = n - 1 ; ~ i ; -- i ) {
int t = count_if ( g [ i ], g [ i ] + n , [ & ]( int x ) { return x <= distanceThreshold ; });
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 func findTheCity ( n int , edges [][] int , distanceThreshold int ) int {
g := make ([][] int , n )
const inf int = 1e7
for i := range g {
g [ i ] = make ([] int , n )
for j := range g [ i ] {
g [ i ][ j ] = inf
}
}
for _ , e := range edges {
f , t , w := e [ 0 ], e [ 1 ], e [ 2 ]
g [ f ][ t ], g [ t ][ f ] = w , w
}
for k := 0 ; k < n ; k ++ {
g [ k ][ k ] = 0
for i := 0 ; i < n ; i ++ {
for j := 0 ; j < n ; j ++ {
g [ i ][ j ] = min ( g [ i ][ j ], g [ i ][ k ] + g [ k ][ j ])
}
}
}
ans , cnt := n , n + 1
for i := n - 1 ; i >= 0 ; i -- {
t := 0
for _ , x := range g [ i ] {
if x <= distanceThreshold {
t ++
}
}
if t < cnt {
cnt , ans = t , i
}
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 function findTheCity ( n : number , edges : number [][], distanceThreshold : number ) : number {
const g : number [][] = Array . from ({ length : n }, () => Array ( n ). fill ( Infinity ));
for ( const [ f , t , w ] of edges ) {
g [ f ][ t ] = g [ t ][ f ] = w ;
}
for ( let k = 0 ; k < n ; ++ k ) {
g [ k ][ k ] = 0 ;
for ( let i = 0 ; i < n ; ++ i ) {
for ( let j = 0 ; j < n ; ++ j ) {
g [ i ][ j ] = Math . min ( g [ i ][ j ], g [ i ][ k ] + g [ k ][ j ]);
}
}
}
let ans = n ,
cnt = n + 1 ;
for ( let i = n - 1 ; i >= 0 ; -- i ) {
const t = g [ i ]. filter ( x => x <= distanceThreshold ). length ;
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 function findTheCity ( n , edges , distanceThreshold ) {
const g = Array . from ({ length : n }, () => Array ( n ). fill ( Infinity ));
for ( const [ f , t , w ] of edges ) {
g [ f ][ t ] = g [ t ][ f ] = w ;
}
for ( let k = 0 ; k < n ; ++ k ) {
g [ k ][ k ] = 0 ;
for ( let i = 0 ; i < n ; ++ i ) {
for ( let j = 0 ; j < n ; ++ j ) {
g [ i ][ j ] = Math . min ( g [ i ][ j ], g [ i ][ k ] + g [ k ][ j ]);
}
}
}
let ans = n ,
cnt = n + 1 ;
for ( let i = n - 1 ; i >= 0 ; -- i ) {
const t = g [ i ]. filter ( x => x <= distanceThreshold ). length ;
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
Solution 3
TypeScript JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48 function findTheCity ( n : number , edges : number [][], distanceThreshold : number ) : number {
const MAX = Number . POSITIVE_INFINITY ;
const g = Array . from ({ length : n }, () => new Map < number , number > ());
const dist : number [] = Array ( n ). fill ( MAX );
const vis : boolean [] = Array ( n ). fill ( false );
for ( const [ f , t , w ] of edges ) {
g [ f ]. set ( t , w );
g [ t ]. set ( f , w );
}
const dijkstra = ( u : number ) : number => {
dist . fill ( MAX );
vis . fill ( false );
dist [ u ] = 0 ;
const pq = new MinPriorityQueue ();
pq . enqueue ( u , 0 );
while ( ! pq . isEmpty ()) {
const u = pq . dequeue (). element ;
if ( vis [ u ]) continue ;
vis [ u ] = true ;
for ( const [ v , w ] of g [ u ]) {
if ( vis [ v ]) continue ;
const wNext = dist [ u ] + w ;
if ( wNext < dist [ v ]) {
dist [ v ] = wNext ;
pq . enqueue ( v , dist [ v ]);
}
}
}
return dist . filter ( d => d <= distanceThreshold ). length ;
};
let ans = n ;
let cnt = MAX ;
for ( let i = n - 1 ; i >= 0 ; -- i ) {
const t = dijkstra ( i );
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48 export function findTheCity ( n , edges , distanceThreshold ) {
const MAX = Number . POSITIVE_INFINITY ;
const g = Array . from ({ length : n }, () => new Map ());
const dist = Array ( n ). fill ( MAX );
const vis = Array ( n ). fill ( false );
for ( const [ f , t , w ] of edges ) {
g [ f ]. set ( t , w );
g [ t ]. set ( f , w );
}
const dijkstra = u => {
dist . fill ( MAX );
vis . fill ( false );
dist [ u ] = 0 ;
const pq = new MinPriorityQueue ();
pq . enqueue ( u , 0 );
while ( ! pq . isEmpty ()) {
const u = pq . dequeue (). element ;
if ( vis [ u ]) continue ;
vis [ u ] = true ;
for ( const [ v , w ] of g [ u ]) {
if ( vis [ v ]) continue ;
const wNext = dist [ u ] + w ;
if ( wNext < dist [ v ]) {
dist [ v ] = wNext ;
pq . enqueue ( v , dist [ v ]);
}
}
}
return dist . filter ( d => d <= distanceThreshold ). length ;
};
let ans = n ;
let cnt = MAX ;
for ( let i = n - 1 ; i >= 0 ; -- i ) {
const t = dijkstra ( i );
if ( t < cnt ) {
cnt = t ;
ans = i ;
}
}
return ans ;
}
GitHub