1311. Get Watched Videos by Your Friends

Description

There are n people, each person has a unique id between 0 and n-1. Given the arrays watchedVideos and friends, where watchedVideos[i] and friends[i] contain the list of watched videos and the list of friends respectively for the person with id = i.

Level 1 of videos are all watched videos by your friends, level 2 of videos are all watched videos by the friends of your friends and so on. In general, the level k of videos are all watched videos by people with the shortest path exactly equal to k with you. Given your id and the level of videos, return the list of videos ordered by their frequencies (increasing). For videos with the same frequency order them alphabetically from least to greatest.

Example 1:

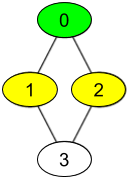
Input: watchedVideos = [["A","B"],["C"],["B","C"],["D"]], friends = [[1,2],[0,3],[0,3],[1,2]], id = 0, level = 1
Output: ["B","C"] 
Explanation: 
You have id = 0 (green color in the figure) and your friends are (yellow color in the figure):
Person with id = 1 -> watchedVideos = ["C"] 
Person with id = 2 -> watchedVideos = ["B","C"] 
The frequencies of watchedVideos by your friends are: 
B -> 1 
C -> 2

Example 2:

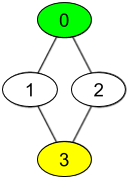
Input: watchedVideos = [["A","B"],["C"],["B","C"],["D"]], friends = [[1,2],[0,3],[0,3],[1,2]], id = 0, level = 2
Output: ["D"]
Explanation: 
You have id = 0 (green color in the figure) and the only friend of your friends is the person with id = 3 (yellow color in the figure).

Constraints:

n == watchedVideos.length == friends.length
2 <= n <= 100
1 <= watchedVideos[i].length <= 100
1 <= watchedVideos[i][j].length <= 8
0 <= friends[i].length < n
0 <= friends[i][j] < n
0 <= id < n
1 <= level < n
if friends[i] contains j, then friends[j] contains i

Solutions

Solution 1: BFS

We can use the Breadth-First Search (BFS) method to start from $\textit{id}$ and find all friends at a distance of $\textit{level}$, then count the videos watched by these friends.

Specifically, we can use a queue $\textit{q}$ to store the friends at the current level. Initially, add $\textit{id}$ to the queue $\textit{q}$. Use a hash table or a boolean array $\textit{vis}$ to record the friends that have already been visited. Then, perform $\textit{level}$ iterations, in each iteration dequeue all friends from the queue and enqueue their friends until all friends at distance $\textit{level}$ are found.

Next, we use a hash table $\textit{cnt}$ to count the videos watched by these friends and their frequencies. Finally, sort the key-value pairs in the hash table in ascending order by frequency, and if frequencies are the same, sort by video name in ascending order. Return the sorted list of video names.

Time complexity is $O(n + m + v \times \log v)$, and space complexity is $O(n + v)$. Here, $n$ and $m$ are the lengths of the arrays $\textit{watchedVideos}$ and $\textit{friends}$, respectively, and $v$ is the total number of videos watched by all friends.

Python3JavaC++GoTypeScript

class Solution:
    def watchedVideosByFriends(
        self,
        watchedVideos: List[List[str]],
        friends: List[List[int]],
        id: int,
        level: int,
    ) -> List[str]:
        q = deque([id])
        vis = {id}
        for _ in range(level):
            for _ in range(len(q)):
                i = q.popleft()
                for j in friends[i]:
                    if j not in vis:
                        vis.add(j)
                        q.append(j)
        cnt = Counter()
        for i in q:
            for v in watchedVideos[i]:
                cnt[v] += 1
        return sorted(cnt.keys(), key=lambda k: (cnt[k], k))

class Solution {
    public List<String> watchedVideosByFriends(
        List<List<String>> watchedVideos, int[][] friends, int id, int level) {
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(id);
        int n = friends.length;
        boolean[] vis = new boolean[n];
        vis[id] = true;
        while (level-- > 0) {
            for (int k = q.size(); k > 0; --k) {
                int i = q.poll();
                for (int j : friends[i]) {
                    if (!vis[j]) {
                        vis[j] = true;
                        q.offer(j);
                    }
                }
            }
        }
        Map<String, Integer> cnt = new HashMap<>();
        for (int i : q) {
            for (var v : watchedVideos.get(i)) {
                cnt.merge(v, 1, Integer::sum);
            }
        }
        List<String> ans = new ArrayList<>(cnt.keySet());
        ans.sort((a, b) -> {
            int x = cnt.get(a), y = cnt.get(b);
            return x == y ? a.compareTo(b) : Integer.compare(x, y);
        });
        return ans;
    }
}

class Solution {
public:
    vector<string> watchedVideosByFriends(vector<vector<string>>& watchedVideos, vector<vector<int>>& friends, int id, int level) {
        queue<int> q{{id}};
        int n = friends.size();
        vector<bool> vis(n);
        vis[id] = true;
        while (level--) {
            for (int k = q.size(); k; --k) {
                int i = q.front();
                q.pop();
                for (int j : friends[i]) {
                    if (!vis[j]) {
                        vis[j] = true;
                        q.push(j);
                    }
                }
            }
        }
        unordered_map<string, int> cnt;
        while (!q.empty()) {
            int i = q.front();
            q.pop();
            for (const auto& v : watchedVideos[i]) {
                cnt[v]++;
            }
        }
        vector<string> ans;
        for (const auto& [key, _] : cnt) {
            ans.push_back(key);
        }
        sort(ans.begin(), ans.end(), [&cnt](const string& a, const string& b) {
            return cnt[a] == cnt[b] ? a < b : cnt[a] < cnt[b];
        });
        return ans;
    }
};

func watchedVideosByFriends(watchedVideos [][]string, friends [][]int, id int, level int) []string {
    q := []int{id}
    n := len(friends)
    vis := make([]bool, n)
    vis[id] = true
    for level > 0 {
        level--
        nextQ := []int{}
        for _, i := range q {
            for _, j := range friends[i] {
                if !vis[j] {
                    vis[j] = true
                    nextQ = append(nextQ, j)
                }
            }
        }
        q = nextQ
    }
    cnt := make(map[string]int)
    for _, i := range q {
        for _, v := range watchedVideos[i] {
            cnt[v]++
        }
    }
    ans := []string{}
    for key := range cnt {
        ans = append(ans, key)
    }
    sort.Slice(ans, func(i, j int) bool {
        if cnt[ans[i]] == cnt[ans[j]] {
            return ans[i] < ans[j]
        }
        return cnt[ans[i]] < cnt[ans[j]]
    })
    return ans
}

function watchedVideosByFriends(
    watchedVideos: string[][],
    friends: number[][],
    id: number,
    level: number,
): string[] {
    let q: number[] = [id];
    const n: number = friends.length;
    const vis: boolean[] = Array(n).fill(false);
    vis[id] = true;
    while (level-- > 0) {
        const nq: number[] = [];
        for (const i of q) {
            for (const j of friends[i]) {
                if (!vis[j]) {
                    vis[j] = true;
                    nq.push(j);
                }
            }
        }
        q = nq;
    }
    const cnt: { [key: string]: number } = {};
    for (const i of q) {
        for (const v of watchedVideos[i]) {
            cnt[v] = (cnt[v] || 0) + 1;
        }
    }
    const ans: string[] = Object.keys(cnt);
    ans.sort((a, b) => {
        if (cnt[a] === cnt[b]) {
            return a.localeCompare(b);
        }
        return cnt[a] - cnt[b];
    });
    return ans;
}

1311. Get Watched Videos by Your Friends

Description

Solutions

Solution 1: BFS

Comments