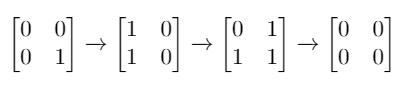Skip to content

1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

Description

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighbors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

A binary matrix is a matrix with all cells equal to 0 or 1 only.

A zero matrix is a matrix with all cells equal to 0.

 

Example 1:

Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We do not need to change it.

Example 3:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix cannot be a zero matrix.

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 3
  • mat[i][j] is either 0 or 1.

Solutions

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def minFlips(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        state = sum(1 << (i * n + j) for i in range(m) for j in range(n) if mat[i][j])
        q = deque([state])
        vis = {state}
        ans = 0
        dirs = [0, -1, 0, 1, 0, 0]
        while q:
            for _ in range(len(q)):
                state = q.popleft()
                if state == 0:
                    return ans
                for i in range(m):
                    for j in range(n):
                        nxt = state
                        for k in range(5):
                            x, y = i + dirs[k], j + dirs[k + 1]
                            if not 0 <= x < m or not 0 <= y < n:
                                continue
                            if nxt & (1 << (x * n + y)):
                                nxt -= 1 << (x * n + y)
                            else:
                                nxt |= 1 << (x * n + y)
                        if nxt not in vis:
                            vis.add(nxt)
                            q.append(nxt)
            ans += 1
        return -1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
    public int minFlips(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int state = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1) {
                    state |= 1 << (i * n + j);
                }
            }
        }
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(state);
        Set<Integer> vis = new HashSet<>();
        vis.add(state);
        int ans = 0;
        int[] dirs = {0, -1, 0, 1, 0, 0};
        while (!q.isEmpty()) {
            for (int t = q.size(); t > 0; --t) {
                state = q.poll();
                if (state == 0) {
                    return ans;
                }
                for (int i = 0; i < m; ++i) {
                    for (int j = 0; j < n; ++j) {
                        int nxt = state;
                        for (int k = 0; k < 5; ++k) {
                            int x = i + dirs[k], y = j + dirs[k + 1];
                            if (x < 0 || x >= m || y < 0 || y >= n) {
                                continue;
                            }
                            if ((nxt & (1 << (x * n + y))) != 0) {
                                nxt -= 1 << (x * n + y);
                            } else {
                                nxt |= 1 << (x * n + y);
                            }
                        }
                        if (!vis.contains(nxt)) {
                            vis.add(nxt);
                            q.offer(nxt);
                        }
                    }
                }
            }
            ++ans;
        }
        return -1;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    int minFlips(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        int state = 0;
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (mat[i][j])
                    state |= (1 << (i * n + j));
        queue<int> q{{state}};
        unordered_set<int> vis{{state}};
        int ans = 0;
        vector<int> dirs = {0, -1, 0, 1, 0, 0};
        while (!q.empty()) {
            for (int t = q.size(); t; --t) {
                state = q.front();
                if (state == 0) return ans;
                q.pop();
                for (int i = 0; i < m; ++i) {
                    for (int j = 0; j < n; ++j) {
                        int nxt = state;
                        for (int k = 0; k < 5; ++k) {
                            int x = i + dirs[k], y = j + dirs[k + 1];
                            if (x < 0 || x >= m || y < 0 || y >= n) continue;
                            if ((nxt & (1 << (x * n + y))) != 0)
                                nxt -= 1 << (x * n + y);
                            else
                                nxt |= 1 << (x * n + y);
                        }
                        if (!vis.count(nxt)) {
                            vis.insert(nxt);
                            q.push(nxt);
                        }
                    }
                }
            }
            ++ans;
        }
        return -1;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
func minFlips(mat [][]int) int {
    m, n := len(mat), len(mat[0])
    state := 0
    for i, row := range mat {
        for j, v := range row {
            if v == 1 {
                state |= 1 << (i*n + j)
            }
        }
    }
    q := []int{state}
    vis := map[int]bool{state: true}
    ans := 0
    dirs := []int{0, -1, 0, 1, 0, 0}
    for len(q) > 0 {
        for t := len(q); t > 0; t-- {
            state = q[0]
            if state == 0 {
                return ans
            }
            q = q[1:]
            for i := 0; i < m; i++ {
                for j := 0; j < n; j++ {
                    nxt := state
                    for k := 0; k < 5; k++ {
                        x, y := i+dirs[k], j+dirs[k+1]
                        if x < 0 || x >= m || y < 0 || y >= n {
                            continue
                        }
                        if (nxt & (1 << (x*n + y))) != 0 {
                            nxt -= 1 << (x*n + y)
                        } else {
                            nxt |= 1 << (x*n + y)
                        }
                    }
                    if !vis[nxt] {
                        vis[nxt] = true
                        q = append(q, nxt)
                    }
                }
            }
        }
        ans++
    }
    return -1
}

Comments