Skip to content

1273. Delete Tree Nodes πŸ”’

Description

A tree rooted at node 0 is given as follows:

  • The number of nodes is nodes;
  • The value of the ith node is value[i];
  • The parent of the ith node is parent[i].

Remove every subtree whose sum of values of nodes is zero.

Return the number of the remaining nodes in the tree.

 

Example 1:

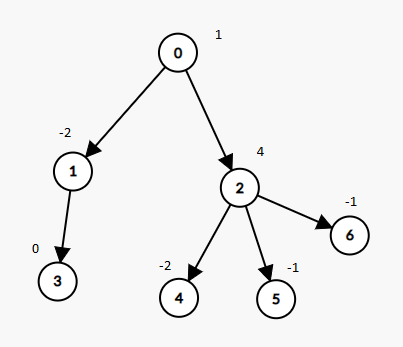
Input: nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-1]
Output: 2

Example 2:

Input: nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-2]
Output: 6

 

Constraints:

  • 1 <= nodes <= 104
  • parent.length == nodes
  • 0 <= parent[i] <= nodes - 1
  • parent[0] == -1 which indicates that 0 is the root.
  • value.length == nodes
  • -105 <= value[i] <= 105
  • The given input is guaranteed to represent a valid tree.

Solutions

Solution 1: DFS

First, we convert the tree into a graph $g$, where $g[i]$ represents all the child nodes of node $i$.

Then we design a function $dfs(i)$, which represents the number of nodes and the sum of the weights in the subtree rooted at node $i$. The answer is $dfs(0)[1]$.

In this function, we recursively calculate the number of nodes and the sum of the weights in the subtree rooted at each child node $j$, and then accumulate these values. If the accumulated value is zero, we set the number of nodes in this subtree to zero. Finally, we return the number of nodes and the sum of the weights in the subtree rooted at node $i$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes in the tree.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def deleteTreeNodes(self, nodes: int, parent: List[int], value: List[int]) -> int:
        def dfs(i):
            s, m = value[i], 1
            for j in g[i]:
                t, n = dfs(j)
                s += t
                m += n
            if s == 0:
                m = 0
            return (s, m)

        g = defaultdict(list)
        for i in range(1, nodes):
            g[parent[i]].append(i)
        return dfs(0)[1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    private List<Integer>[] g;
    private int[] value;

    public int deleteTreeNodes(int nodes, int[] parent, int[] value) {
        g = new List[nodes];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int i = 1; i < nodes; ++i) {
            g[parent[i]].add(i);
        }
        this.value = value;
        return dfs(0)[1];
    }

    private int[] dfs(int i) {
        int[] res = new int[] {value[i], 1};
        for (int j : g[i]) {
            int[] t = dfs(j);
            res[0] += t[0];
            res[1] += t[1];
        }
        if (res[0] == 0) {
            res[1] = 0;
        }
        return res;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int deleteTreeNodes(int nodes, vector<int>& parent, vector<int>& value) {
        vector<vector<int>> g(nodes);
        for (int i = 1; i < nodes; ++i) {
            g[parent[i]].emplace_back(i);
        }
        function<pair<int, int>(int)> dfs = [&](int i) -> pair<int, int> {
            int s = value[i], m = 1;
            for (int j : g[i]) {
                auto [t, n] = dfs(j);
                s += t;
                m += n;
            }
            if (s == 0) {
                m = 0;
            }
            return pair<int, int>{s, m};
        };
        return dfs(0).second;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
func deleteTreeNodes(nodes int, parent []int, value []int) int {
    g := make([][]int, nodes)
    for i := 1; i < nodes; i++ {
        g[parent[i]] = append(g[parent[i]], i)
    }
    type pair struct{ s, n int }
    var dfs func(int) pair
    dfs = func(i int) pair {
        s, m := value[i], 1
        for _, j := range g[i] {
            t := dfs(j)
            s += t.s
            m += t.n
        }
        if s == 0 {
            m = 0
        }
        return pair{s, m}
    }
    return dfs(0).n
}

Comments