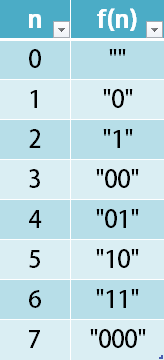1256. Encode Number 🔒

Description

Given a non-negative integer num, Return its encoding string.

The encoding is done by converting the integer to a string using a secret function that you should deduce from the following table:

 

Example 1:

Input: num = 23

Output: "1000"

Example 2:

Input: num = 107

Output: "101100"

 

Constraints:

• 0 <= num <= 10^9

Solutions

Solution 1: Bit Manipulation

We add one to $num$, then convert it to a binary string and remove the highest bit $1$.

The time complexity is $O(\log n)$, and the space complexity is $O(\log n)$. Where $n$ is the size of $num$.

Python3JavaC++GoTypeScript

class Solution:
    def encode(self, num: int) -> str:
        return bin(num + 1)[3:]

class Solution {
    public String encode(int num) {
        return Integer.toBinaryString(num + 1).substring(1);
    }
}

class Solution {
public:
    string encode(int num) {
        bitset<32> bs(++num);
        string ans = bs.to_string();
        int i = 0;
        while (ans[i] == '0') {
            ++i;
        }
        return ans.substr(i + 1);
    }
};

func encode(num int) string {
    num++
    s := strconv.FormatInt(int64(num), 2)
    return s[1:]
}

function encode(num: number): string {
    ++num;
    let s = num.toString(2);
    return s.slice(1);
}

Comments