118. Pascal's Triangle

Description

Given an integer numRows, return the first numRows of Pascal's triangle.

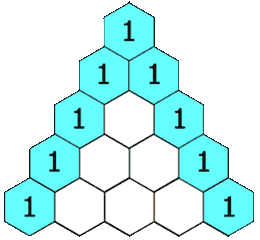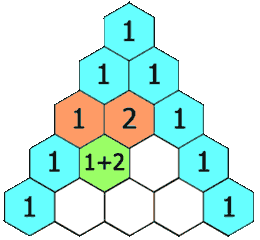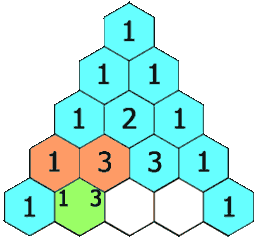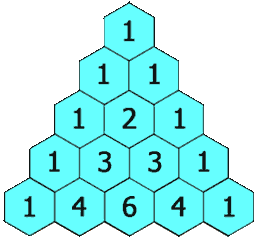
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:

Example 1:

Input: numRows = 5
Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

Example 2:

Input: numRows = 1
Output: [[1]]

Constraints:

1 <= numRows <= 30

Solutions

Solution 1: Simulation

First, we create an answer array \(f\), and then set the first row of \(f\) to \([1]\). Next, starting from the second row, the first and last elements of each row are \(1\), and the other elements are calculated by \(f[i][j] = f[i - 1][j - 1] + f[i - 1][j]\).

The time complexity is \(O(n^2)\), and the space complexity is \(O(n^2)\). Here, \(n\) is the number of rows.

Python3JavaC++GoTypeScriptRustJavaScript

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        f = [[1]]
        for i in range(numRows - 1):
            g = [1] + [a + b for a, b in pairwise(f[-1])] + [1]
            f.append(g)
        return f

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> f = new ArrayList<>();
        f.add(List.of(1));
        for (int i = 0; i < numRows - 1; ++i) {
            List<Integer> g = new ArrayList<>();
            g.add(1);
            for (int j = 0; j < f.get(i).size() - 1; ++j) {
                g.add(f.get(i).get(j) + f.get(i).get(j + 1));
            }
            g.add(1);
            f.add(g);
        }
        return f;
    }
}

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> f;
        f.push_back(vector<int>(1, 1));
        for (int i = 0; i < numRows - 1; ++i) {
            vector<int> g;
            g.push_back(1);
            for (int j = 0; j < f[i].size() - 1; ++j) {
                g.push_back(f[i][j] + f[i][j + 1]);
            }
            g.push_back(1);
            f.push_back(g);
        }
        return f;
    }
};

func generate(numRows int) [][]int {
    f := [][]int{[]int{1}}
    for i := 0; i < numRows-1; i++ {
        g := []int{1}
        for j := 0; j < len(f[i])-1; j++ {
            g = append(g, f[i][j]+f[i][j+1])
        }
        g = append(g, 1)
        f = append(f, g)
    }
    return f
}

function generate(numRows: number): number[][] {
    const f: number[][] = [[1]];
    for (let i = 0; i < numRows - 1; ++i) {
        const g: number[] = [1];
        for (let j = 0; j < f[i].length - 1; ++j) {
            g.push(f[i][j] + f[i][j + 1]);
        }
        g.push(1);
        f.push(g);
    }
    return f;
}

impl Solution {
    #[allow(dead_code)]
    pub fn generate(num_rows: i32) -> Vec<Vec<i32>> {
        let mut ret_vec: Vec<Vec<i32>> = Vec::new();
        let mut cur_vec: Vec<i32> = Vec::new();

        for i in 0..num_rows as usize {
            let mut new_vec: Vec<i32> = vec![1; i + 1];
            for j in 1..i {
                new_vec[j] = cur_vec[j - 1] + cur_vec[j];
            }
            cur_vec = new_vec.clone();
            ret_vec.push(new_vec);
        }

        ret_vec
    }
}

/**
 * @param {number} numRows
 * @return {number[][]}
 */
var generate = function (numRows) {
    const f = [[1]];
    for (let i = 0; i < numRows - 1; ++i) {
        const g = [1];
        for (let j = 0; j < f[i].length - 1; ++j) {
            g.push(f[i][j] + f[i][j + 1]);
        }
        g.push(1);
        f.push(g);
    }
    return f;
};

118. Pascal's Triangle

Description

Solutions

Solution 1: Simulation

Comments