1120. Maximum Average Subtree 🔒

Description

Given the root of a binary tree, return the maximum average value of a subtree of that tree. Answers within 10-5 of the actual answer will be accepted.

A subtree of a tree is any node of that tree plus all its descendants.

The average value of a tree is the sum of its values, divided by the number of nodes.

 

Example 1:

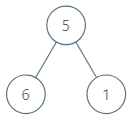
Input: root = [5,6,1]
Output: 6.00000
Explanation: 
For the node with value = 5 we have an average of (5 + 6 + 1) / 3 = 4.
For the node with value = 6 we have an average of 6 / 1 = 6.
For the node with value = 1 we have an average of 1 / 1 = 1.
So the answer is 6 which is the maximum.

Example 2:

Input: root = [0,null,1]
Output: 1.00000

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 0 <= Node.val <= 105

Solutions

Solution 1: Recursion

We can use a recursive method. For each node, we calculate the sum and count of the nodes in the subtree rooted at that node, then calculate the average, compare it with the current maximum, and update the maximum if necessary.

Therefore, we design a function dfs(root) that represents the sum and count of nodes in the subtree rooted at root. The return value is an array of length 2, where the first element represents the sum of nodes, and the second element represents the count of nodes.

The recursive process of the function dfs(root) is as follows:

• If root is null, return [0, 0];
• Otherwise, calculate the sum and count of nodes in the left subtree of root, denoted as [ls, ln]; calculate the sum and count of nodes in the right subtree of root, denoted as [rs, rn]. The sum of nodes in the subtree rooted at root is root.val + ls + rs, and the count of nodes is 1 + ln + rn. Calculate the average, compare it with the current maximum, and update the maximum if necessary;
• Return [root.val + ls + rs, 1 + ln + rn].

Finally, return the maximum value.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.

Python3JavaC++Go

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maximumAverageSubtree(self, root: Optional[TreeNode]) -> float:
        def dfs(root):
            if root is None:
                return 0, 0
            ls, ln = dfs(root.left)
            rs, rn = dfs(root.right)
            s = root.val + ls + rs
            n = 1 + ln + rn
            nonlocal ans
            ans = max(ans, s / n)
            return s, n

        ans = 0
        dfs(root)
        return ans

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private double ans;

    public double maximumAverageSubtree(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int[] dfs(TreeNode root) {
        if (root == null) {
            return new int[2];
        }
        var l = dfs(root.left);
        var r = dfs(root.right);
        int s = root.val + l[0] + r[0];
        int n = 1 + l[1] + r[1];
        ans = Math.max(ans, s * 1.0 / n);
        return new int[] {s, n};
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    double maximumAverageSubtree(TreeNode* root) {
        double ans = 0;
        function<pair<int, int>(TreeNode*)> dfs = [&](TreeNode* root) -> pair<int, int> {
            if (!root) {
                return {0, 0};
            }
            auto [ls, ln] = dfs(root->left);
            auto [rs, rn] = dfs(root->right);
            int s = root->val + ls + rs;
            int n = 1 + ln + rn;
            ans = max(ans, s * 1.0 / n);
            return {s, n};
        };
        dfs(root);
        return ans;
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maximumAverageSubtree(root *TreeNode) (ans float64) {
    var dfs func(*TreeNode) [2]int
    dfs = func(root *TreeNode) [2]int {
        if root == nil {
            return [2]int{}
        }
        l, r := dfs(root.Left), dfs(root.Right)
        s := root.Val + l[0] + r[0]
        n := 1 + l[1] + r[1]
        ans = math.Max(ans, float64(s)/float64(n))
        return [2]int{s, n}
    }
    dfs(root)
    return
}

Comments