Skip to content

1104. Path In Zigzag Labelled Binary Tree

Description

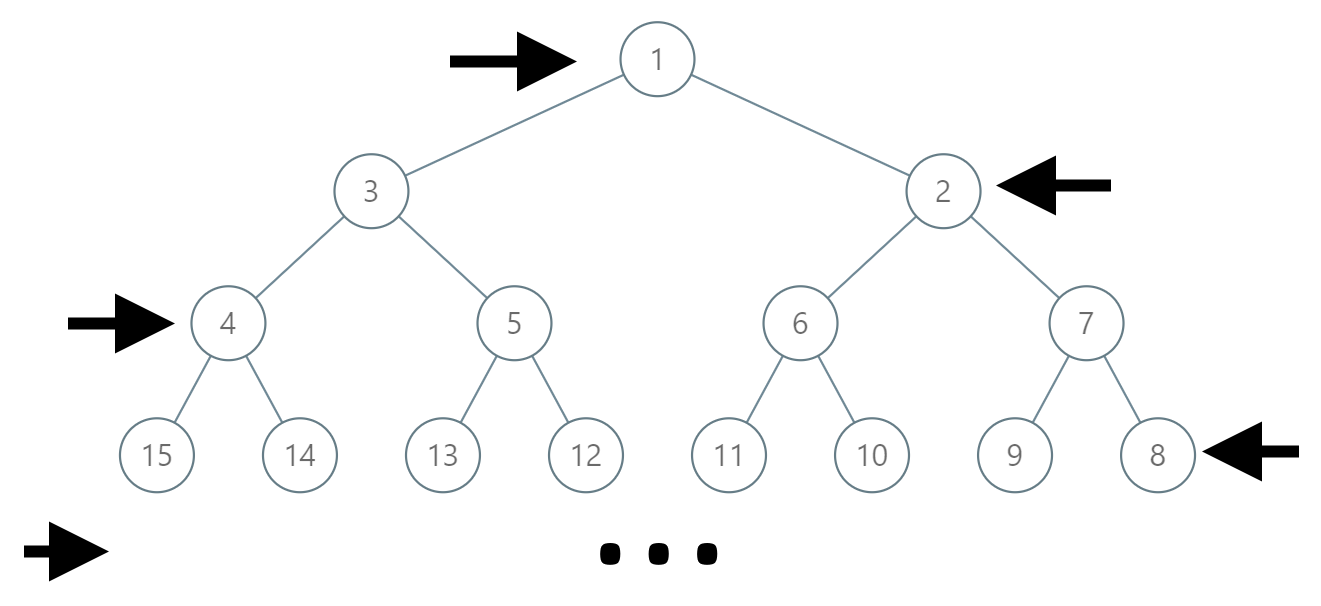
In an infinite binary tree where every node has two children, the nodes are labelled in row order.

In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.

Given the label of a node in this tree, return the labels in the path from the root of the tree to the node with that label.

 

Example 1:

Input: label = 14
Output: [1,3,4,14]

Example 2:

Input: label = 26
Output: [1,2,6,10,26]

 

Constraints:

  • 1 <= label <= 10^6

Solutions

Solution 1: Mathematics

For a complete binary tree, the number of nodes in the $i$th row is $2^{i-1}$, and the range of node labels in the $i$th row is $[2^{i-1}, 2^i - 1]$. In the problem, for odd-numbered rows, the nodes are labeled from left to right, while for even-numbered rows, the nodes are labeled from right to left. Therefore, for the node $label$ in the $i$th row, its complementary node label is $2^{i-1} + 2^i - 1 - label$. So the actual parent node label of node $label$ is $(2^{i-1} + 2^i - 1 - label) / 2$. We can find the path from the root node to node $label$ by continuously finding the complementary node label and the parent node label until we reach the root node.

Finally, we need to reverse the path, because the problem requires the path from the root node to node $label$.

The time complexity is $O(\log n)$, where $n$ is the label of the node. Ignoring the space consumption of the answer, the space complexity is $O(1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def pathInZigZagTree(self, label: int) -> List[int]:
        x = i = 1
        while (x << 1) <= label:
            x <<= 1
            i += 1
        ans = [0] * i
        while i:
            ans[i - 1] = label
            label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1
            i -= 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public List<Integer> pathInZigZagTree(int label) {
        int x = 1, i = 1;
        while ((x << 1) <= label) {
            x <<= 1;
            ++i;
        }
        List<Integer> ans = new ArrayList<>();
        for (; i > 0; --i) {
            ans.add(label);
            label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1;
        }
        Collections.reverse(ans);
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> pathInZigZagTree(int label) {
        int x = 1, i = 1;
        while ((x << 1) <= label) {
            x <<= 1;
            ++i;
        }
        vector<int> ans;
        for (; i > 0; --i) {
            ans.push_back(label);
            label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1;
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
func pathInZigZagTree(label int) (ans []int) {
    x, i := 1, 1
    for x<<1 <= label {
        x <<= 1
        i++
    }
    for ; i > 0; i-- {
        ans = append(ans, label)
        label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1
    }
    for i, j := 0, len(ans)-1; i < j; i, j = i+1, j-1 {
        ans[i], ans[j] = ans[j], ans[i]
    }
    return
}

Comments