Binary Tree
Depth-First Search
Tree
Description
Given the root of a binary tree and an integer limit, delete all insufficient nodes in the tree simultaneously, and return the root of the resulting binary tree .
A node is insufficient if every root to leaf path intersecting this node has a sum strictly less than limit.
A leaf is a node with no children.
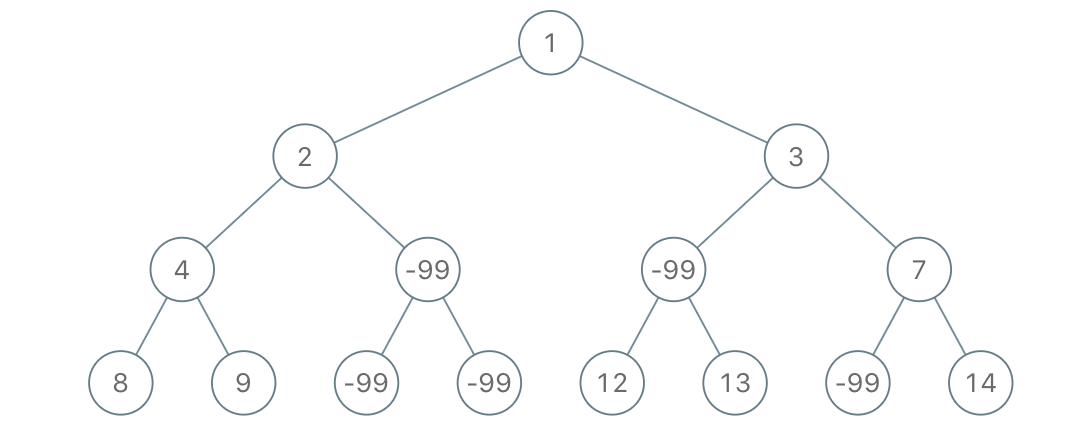
Example 1:
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
Output: [1,2,3,4,null,null,7,8,9,null,14]
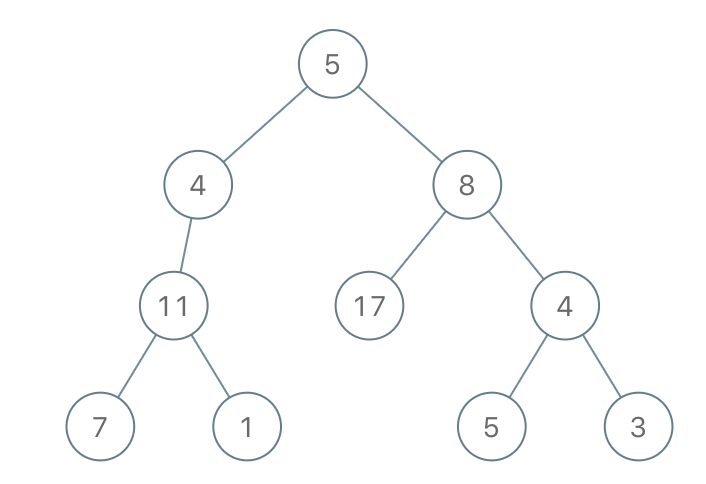
Example 2:
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
Output: [5,4,8,11,null,17,4,7,null,null,null,5]
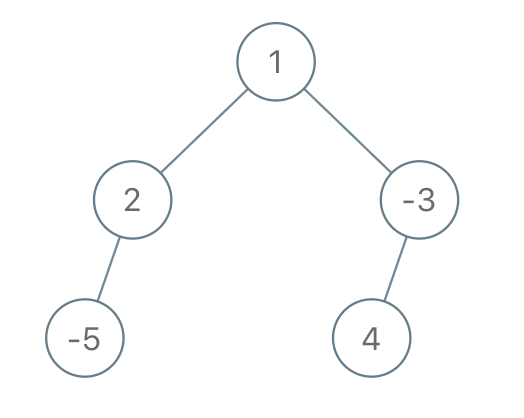
Example 3:
Input: root = [1,2,-3,-5,null,4,null], limit = -1
Output: [1,null,-3,4]
Constraints:
The number of nodes in the tree is in the range [1, 5000].
-105 <= Node.val <= 105 -109 <= limit <= 109
Solutions
Solution 1
Python3 Java C++ Go TypeScript JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def sufficientSubset (
self , root : Optional [ TreeNode ], limit : int
) -> Optional [ TreeNode ]:
if root is None :
return None
limit -= root . val
if root . left is None and root . right is None :
return None if limit > 0 else root
root . left = self . sufficientSubset ( root . left , limit )
root . right = self . sufficientSubset ( root . right , limit )
return None if root . left is None and root . right is None else root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode sufficientSubset ( TreeNode root , int limit ) {
if ( root == null ) {
return null ;
}
limit -= root . val ;
if ( root . left == null && root . right == null ) {
return limit > 0 ? null : root ;
}
root . left = sufficientSubset ( root . left , limit );
root . right = sufficientSubset ( root . right , limit );
return root . left == null && root . right == null ? null : root ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * sufficientSubset ( TreeNode * root , int limit ) {
if ( ! root ) {
return nullptr ;
}
limit -= root -> val ;
if ( ! root -> left && ! root -> right ) {
return limit > 0 ? nullptr : root ;
}
root -> left = sufficientSubset ( root -> left , limit );
root -> right = sufficientSubset ( root -> right , limit );
return ! root -> left && ! root -> right ? nullptr : root ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func sufficientSubset ( root * TreeNode , limit int ) * TreeNode {
if root == nil {
return nil
}
limit -= root . Val
if root . Left == nil && root . Right == nil {
if limit > 0 {
return nil
}
return root
}
root . Left = sufficientSubset ( root . Left , limit )
root . Right = sufficientSubset ( root . Right , limit )
if root . Left == nil && root . Right == nil {
return nil
}
return root
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function sufficientSubset ( root : TreeNode | null , limit : number ) : TreeNode | null {
if ( root === null ) {
return null ;
}
limit -= root . val ;
if ( root . left === null && root . right === null ) {
return limit > 0 ? null : root ;
}
root . left = sufficientSubset ( root . left , limit );
root . right = sufficientSubset ( root . right , limit );
return root . left === null && root . right === null ? null : root ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 /**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} limit
* @return {TreeNode}
*/
var sufficientSubset = function ( root , limit ) {
if ( root === null ) {
return null ;
}
limit -= root . val ;
if ( root . left === null && root . right === null ) {
return limit > 0 ? null : root ;
}
root . left = sufficientSubset ( root . left , limit );
root . right = sufficientSubset ( root . right , limit );
return root . left === null && root . right === null ? null : root ;
};