973. 最接近原点的 K 个点

题目描述

给定一个数组 points ，其中 points[i] = [x_i, y_i] 表示 X-Y 平面上的一个点，并且是一个整数 k ，返回离原点 (0,0) 最近的 k 个点。

这里，平面上两点之间的距离是 欧几里德距离（ √(x₁ - x₂)² + (y₁ - y₂)² ）。

你可以按 任何顺序 返回答案。除了点坐标的顺序之外，答案确保是唯一的。

示例 1：

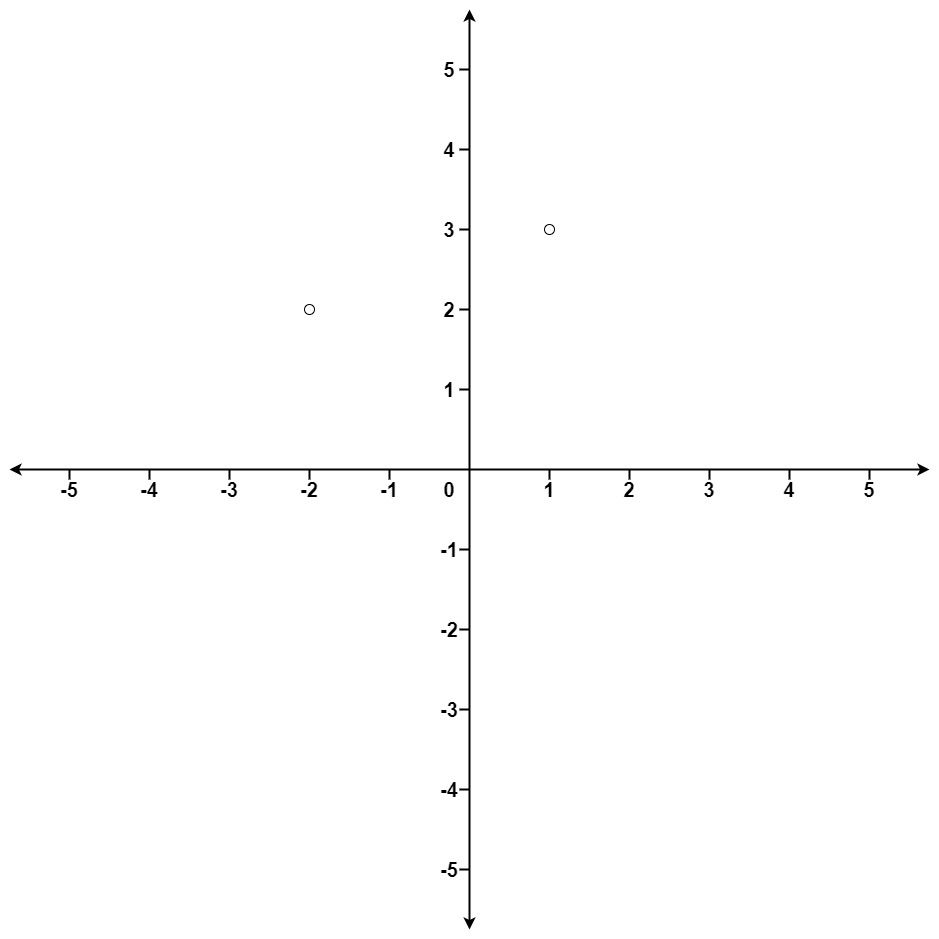
输入：points = [[1,3],[-2,2]], k = 1
输出：[[-2,2]]
解释： 
(1, 3) 和原点之间的距离为 sqrt(10)，
(-2, 2) 和原点之间的距离为 sqrt(8)，
由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]。

示例 2：

输入：points = [[3,3],[5,-1],[-2,4]], k = 2
输出：[[3,3],[-2,4]]
（答案 [[-2,4],[3,3]] 也会被接受。）

提示：

1 <= k <= points.length <= 10⁴
-10⁴ < x_i, y_i < 10⁴

解法

方法一：自定义排序

我们将所有点按照与原点的距离从小到大排序，然后取前 $k$ 个点即可。

时间复杂度 $O(n \times \log n)$，空间复杂度 $O(\log n)$。其中 $n$ 为数组 $\textit{points}$ 的长度。

Python3JavaC++GoTypeScriptRust

class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        points.sort(key=lambda p: hypot(p[0], p[1]))
        return points[:k]

class Solution {
    public int[][] kClosest(int[][] points, int k) {
        Arrays.sort(
            points, (p1, p2) -> Math.hypot(p1[0], p1[1]) - Math.hypot(p2[0], p2[1]) > 0 ? 1 : -1);
        return Arrays.copyOfRange(points, 0, k);
    }
}

class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        sort(points.begin(), points.end(), [](const vector<int>& p1, const vector<int>& p2) {
            return hypot(p1[0], p1[1]) < hypot(p2[0], p2[1]);
        });
        return vector<vector<int>>(points.begin(), points.begin() + k);
    }
};

func kClosest(points [][]int, k int) [][]int {
    sort.Slice(points, func(i, j int) bool {
        return math.Hypot(float64(points[i][0]), float64(points[i][1])) < math.Hypot(float64(points[j][0]), float64(points[j][1]))
    })
    return points[:k]
}

function kClosest(points: number[][], k: number): number[][] {
    points.sort((a, b) => Math.hypot(a[0], a[1]) - Math.hypot(b[0], b[1]));
    return points.slice(0, k);
}

impl Solution {
    pub fn k_closest(mut points: Vec<Vec<i32>>, k: i32) -> Vec<Vec<i32>> {
        points.sort_by(|a, b| {
            let dist_a = f64::hypot(a[0] as f64, a[1] as f64);
            let dist_b = f64::hypot(b[0] as f64, b[1] as f64);
            dist_a.partial_cmp(&dist_b).unwrap()
        });
        points.into_iter().take(k as usize).collect()
    }
}

方法二：优先队列（大根堆）

我们可以使用一个优先队列（大根堆）来维护距离原点最近的 $k$ 个点。

时间复杂度 $O(n \times \log k)$，空间复杂度 $O(k)$。其中 $n$ 为数组 $\textit{points}$ 的长度。

Python3JavaC++GoTypeScript

class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        max_q = []
        for i, (x, y) in enumerate(points):
            dist = math.hypot(x, y)
            heappush(max_q, (-dist, i))
            if len(max_q) > k:
                heappop(max_q)
        return [points[i] for _, i in max_q]

class Solution {
    public int[][] kClosest(int[][] points, int k) {
        PriorityQueue<int[]> maxQ = new PriorityQueue<>((a, b) -> b[0] - a[0]);
        for (int i = 0; i < points.length; ++i) {
            int x = points[i][0], y = points[i][1];
            maxQ.offer(new int[] {x * x + y * y, i});
            if (maxQ.size() > k) {
                maxQ.poll();
            }
        }
        int[][] ans = new int[k][2];
        for (int i = 0; i < k; ++i) {
            ans[i] = points[maxQ.poll()[1]];
        }
        return ans;
    }
}

class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        priority_queue<pair<double, int>> pq;
        for (int i = 0, n = points.size(); i < n; ++i) {
            double dist = hypot(points[i][0], points[i][1]);
            pq.push({dist, i});
            if (pq.size() > k) {
                pq.pop();
            }
        }
        vector<vector<int>> ans;
        while (!pq.empty()) {
            ans.push_back(points[pq.top().second]);
            pq.pop();
        }
        return ans;
    }
};

func kClosest(points [][]int, k int) [][]int {
    maxQ := hp{}
    for i, p := range points {
        dist := math.Hypot(float64(p[0]), float64(p[1]))
        heap.Push(&maxQ, pair{dist, i})
        if len(maxQ) > k {
            heap.Pop(&maxQ)
        }
    }
    ans := make([][]int, k)
    for i, p := range maxQ {
        ans[i] = points[p.i]
    }
    return ans
}

type pair struct {
    dist float64
    i    int
}

type hp []pair

func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool {
    a, b := h[i], h[j]
    return a.dist > b.dist
}
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any)   { *h = append(*h, v.(pair)) }
func (h *hp) Pop() any     { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

function kClosest(points: number[][], k: number): number[][] {
    const maxQ = new MaxPriorityQueue();
    for (const [x, y] of points) {
        const dist = x * x + y * y;
        maxQ.enqueue([x, y], dist);
        if (maxQ.size() > k) {
            maxQ.dequeue();
        }
    }
    return maxQ.toArray().map(item => item.element);
}

方法三：二分查找

我们注意到，随着距离的增大，点的数量是递增的。这存在一个临界值，使得在这个值之前的点的数量小于等于 $k$，而在这个值之后的点的数量大于 $k$。

因此，我们可以使用二分查找，枚举距离。每一次二分查找，我们统计出距离小于等于当前距离的点的数量，如果数量大于等于 $k$，则说明临界值在左侧，我们令右边界等于当前距离；否则，临界值在右侧，我们令左边界等于当前距禽加一。

二分查找结束后，我们只需要返回距离小于等于左边界的点即可。

时间复杂度 $O(n \times \log M)$，空间复杂度 $O(n)$。其中 $n$ 为数组 $\textit{points}$ 的长度，而 $M$ 为距离的最大值。