
题目描述
给你一个 n * n 的网格 grid ,上面放置着一些 1 x 1 x 1 的正方体。每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
放置好正方体后,任何直接相邻的正方体都会互相粘在一起,形成一些不规则的三维形体。
请你返回最终这些形体的总表面积。
注意:每个形体的底面也需要计入表面积中。
示例 1:

输入:grid = [[1,2],[3,4]]
输出:34
示例 2:
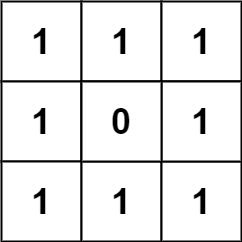
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:32
示例 3:
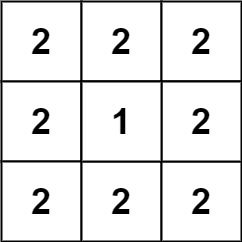
输入:grid = [[2,2,2],[2,1,2],[2,2,2]]
输出:46
提示:
n == grid.lengthn == grid[i].length1 <= n <= 500 <= grid[i][j] <= 50
解法
方法一:遍历,逐个累加
时间复杂度 \(O(n^2)\),空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def surfaceArea(self, grid: List[List[int]]) -> int:
ans = 0
for i, row in enumerate(grid):
for j, v in enumerate(row):
if v:
ans += 2 + v * 4
if i:
ans -= min(v, grid[i - 1][j]) * 2
if j:
ans -= min(v, grid[i][j - 1]) * 2
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public int surfaceArea(int[][] grid) {
int n = grid.length;
int ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] > 0) {
ans += 2 + grid[i][j] * 4;
if (i > 0) {
ans -= Math.min(grid[i][j], grid[i - 1][j]) * 2;
}
if (j > 0) {
ans -= Math.min(grid[i][j], grid[i][j - 1]) * 2;
}
}
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public:
int surfaceArea(vector<vector<int>>& grid) {
int n = grid.size();
int ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j]) {
ans += 2 + grid[i][j] * 4;
if (i) ans -= min(grid[i][j], grid[i - 1][j]) * 2;
if (j) ans -= min(grid[i][j], grid[i][j - 1]) * 2;
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | func surfaceArea(grid [][]int) int {
ans := 0
for i, row := range grid {
for j, v := range row {
if v > 0 {
ans += 2 + v*4
if i > 0 {
ans -= min(v, grid[i-1][j]) * 2
}
if j > 0 {
ans -= min(v, grid[i][j-1]) * 2
}
}
}
}
return ans
}
|



