
题目描述
一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动,你能交换任意两列或是两行的位置。
返回 将这个矩阵变为 “棋盘” 所需的最小移动次数 。如果不存在可行的变换,输出 -1。
“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。
示例 1:
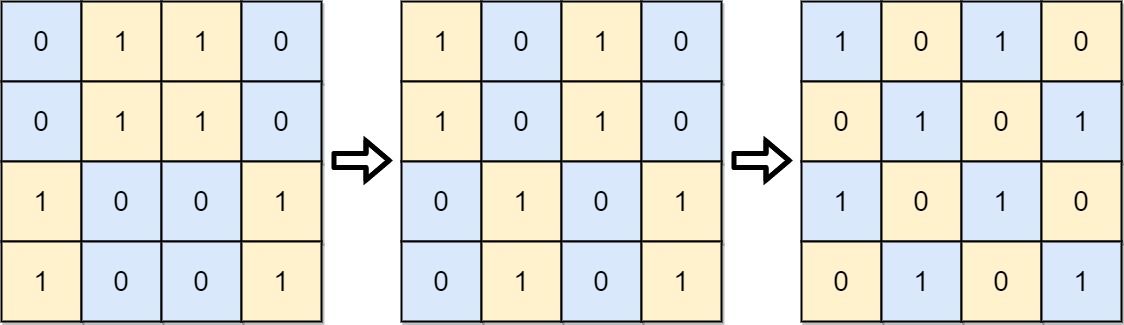
输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
输出: 2
解释:一种可行的变换方式如下,从左到右:
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。
示例 2:
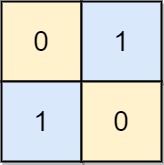
输入: board = [[0, 1], [1, 0]]
输出: 0
解释: 注意左上角的格值为0时也是合法的棋盘,也是合法的棋盘.
示例 3:
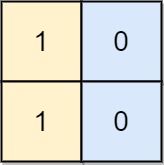
输入: board = [[1, 0], [1, 0]]
输出: -1
解释: 任意的变换都不能使这个输入变为合法的棋盘。
提示:
n == board.lengthn == board[i].length2 <= n <= 30board[i][j] 将只包含 0或 1
解法
方法一:规律观察 + 状态压缩
在一个有效的棋盘中,有且仅有两种“行”。
例如,如果棋盘中有一行为“01010011”,那么任何其它行只能为“01010011”或者“10101100”。列也满足这种性质。
另外,每一行和每一列都有一半 \(0\) 和一半 \(1\)。假设棋盘为 \(n \times n\):
- 若 \(n = 2 \times k\),则每一行和每一列都有 \(k\) 个 \(1\) 和 \(k\) 个 \(0\)。
- 若 \(n = 2 \times k + 1\),则每一行都有 \(k\) 个 \(1\) 和 \(k + 1\) 个 \(0\),或者 \(k + 1\) 个 \(1\) 和 \(k\) 个 \(0\)。
基于以上的结论,我们可以判断一个棋盘是否有效。若有效,可以计算出最小的移动次数。
若 \(n\) 为偶数,最终的合法棋盘有两种可能,即第一行的元素为“010101...”,或者“101010...”。我们计算出这两种可能所需要交换的次数的较小值作为答案。
若 \(n\) 为奇数,那么最终的合法棋盘只有一种可能。如果第一行中 \(0\) 的数目大于 \(1\),那么最终一盘的第一行只能是“01010...”,否则就是“10101...”。同样算出次数作为答案。
时间复杂度 \(O(n^2)\),其中 \(n\) 是棋盘的大小。空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | class Solution:
def movesToChessboard(self, board: List[List[int]]) -> int:
def f(mask, cnt):
ones = mask.bit_count()
if n & 1:
if abs(n - 2 * ones) != 1 or abs(n - 2 * cnt) != 1:
return -1
if ones == n // 2:
return n // 2 - (mask & 0xAAAAAAAA).bit_count()
return (n + 1) // 2 - (mask & 0x55555555).bit_count()
else:
if ones != n // 2 or cnt != n // 2:
return -1
cnt0 = n // 2 - (mask & 0xAAAAAAAA).bit_count()
cnt1 = n // 2 - (mask & 0x55555555).bit_count()
return min(cnt0, cnt1)
n = len(board)
mask = (1 << n) - 1
rowMask = colMask = 0
for i in range(n):
rowMask |= board[0][i] << i
colMask |= board[i][0] << i
revRowMask = mask ^ rowMask
revColMask = mask ^ colMask
sameRow = sameCol = 0
for i in range(n):
curRowMask = curColMask = 0
for j in range(n):
curRowMask |= board[i][j] << j
curColMask |= board[j][i] << j
if curRowMask not in (rowMask, revRowMask) or curColMask not in (
colMask,
revColMask,
):
return -1
sameRow += curRowMask == rowMask
sameCol += curColMask == colMask
t1 = f(rowMask, sameRow)
t2 = f(colMask, sameCol)
return -1 if t1 == -1 or t2 == -1 else t1 + t2
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 | class Solution {
private int n;
public int movesToChessboard(int[][] board) {
n = board.length;
int mask = (1 << n) - 1;
int rowMask = 0, colMask = 0;
for (int i = 0; i < n; ++i) {
rowMask |= board[0][i] << i;
colMask |= board[i][0] << i;
}
int revRowMask = mask ^ rowMask;
int revColMask = mask ^ colMask;
int sameRow = 0, sameCol = 0;
for (int i = 0; i < n; ++i) {
int curRowMask = 0, curColMask = 0;
for (int j = 0; j < n; ++j) {
curRowMask |= board[i][j] << j;
curColMask |= board[j][i] << j;
}
if (curRowMask != rowMask && curRowMask != revRowMask) {
return -1;
}
if (curColMask != colMask && curColMask != revColMask) {
return -1;
}
sameRow += curRowMask == rowMask ? 1 : 0;
sameCol += curColMask == colMask ? 1 : 0;
}
int t1 = f(rowMask, sameRow);
int t2 = f(colMask, sameCol);
return t1 == -1 || t2 == -1 ? -1 : t1 + t2;
}
private int f(int mask, int cnt) {
int ones = Integer.bitCount(mask);
if (n % 2 == 1) {
if (Math.abs(n - ones * 2) != 1 || Math.abs(n - cnt * 2) != 1) {
return -1;
}
if (ones == n / 2) {
return n / 2 - Integer.bitCount(mask & 0xAAAAAAAA);
}
return (n / 2 + 1) - Integer.bitCount(mask & 0x55555555);
} else {
if (ones != n / 2 || cnt != n / 2) {
return -1;
}
int cnt0 = n / 2 - Integer.bitCount(mask & 0xAAAAAAAA);
int cnt1 = n / 2 - Integer.bitCount(mask & 0x55555555);
return Math.min(cnt0, cnt1);
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 | class Solution {
public:
int n;
int movesToChessboard(vector<vector<int>>& board) {
n = board.size();
int mask = (1 << n) - 1;
int rowMask = 0, colMask = 0;
for (int i = 0; i < n; ++i) {
rowMask |= board[0][i] << i;
colMask |= board[i][0] << i;
}
int revRowMask = mask ^ rowMask;
int revColMask = mask ^ colMask;
int sameRow = 0, sameCol = 0;
for (int i = 0; i < n; ++i) {
int curRowMask = 0, curColMask = 0;
for (int j = 0; j < n; ++j) {
curRowMask |= board[i][j] << j;
curColMask |= board[j][i] << j;
}
if (curRowMask != rowMask && curRowMask != revRowMask) return -1;
if (curColMask != colMask && curColMask != revColMask) return -1;
sameRow += curRowMask == rowMask;
sameCol += curColMask == colMask;
}
int t1 = f(rowMask, sameRow);
int t2 = f(colMask, sameCol);
return t1 == -1 || t2 == -1 ? -1 : t1 + t2;
}
int f(int mask, int cnt) {
int ones = __builtin_popcount(mask);
if (n & 1) {
if (abs(n - ones * 2) != 1 || abs(n - cnt * 2) != 1) return -1;
if (ones == n / 2) return n / 2 - __builtin_popcount(mask & 0xAAAAAAAA);
return (n + 1) / 2 - __builtin_popcount(mask & 0x55555555);
} else {
if (ones != n / 2 || cnt != n / 2) return -1;
int cnt0 = (n / 2 - __builtin_popcount(mask & 0xAAAAAAAA));
int cnt1 = (n / 2 - __builtin_popcount(mask & 0x55555555));
return min(cnt0, cnt1);
}
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 | func movesToChessboard(board [][]int) int {
n := len(board)
mask := (1 << n) - 1
rowMask, colMask := 0, 0
for i := 0; i < n; i++ {
rowMask |= board[0][i] << i
colMask |= board[i][0] << i
}
revRowMask := mask ^ rowMask
revColMask := mask ^ colMask
sameRow, sameCol := 0, 0
for i := 0; i < n; i++ {
curRowMask, curColMask := 0, 0
for j := 0; j < n; j++ {
curRowMask |= board[i][j] << j
curColMask |= board[j][i] << j
}
if curRowMask != rowMask && curRowMask != revRowMask {
return -1
}
if curColMask != colMask && curColMask != revColMask {
return -1
}
if curRowMask == rowMask {
sameRow++
}
if curColMask == colMask {
sameCol++
}
}
f := func(mask, cnt int) int {
ones := bits.OnesCount(uint(mask))
if n%2 == 1 {
if abs(n-ones*2) != 1 || abs(n-cnt*2) != 1 {
return -1
}
if ones == n/2 {
return n/2 - bits.OnesCount(uint(mask&0xAAAAAAAA))
}
return (n+1)/2 - bits.OnesCount(uint(mask&0x55555555))
} else {
if ones != n/2 || cnt != n/2 {
return -1
}
cnt0 := n/2 - bits.OnesCount(uint(mask&0xAAAAAAAA))
cnt1 := n/2 - bits.OnesCount(uint(mask&0x55555555))
return min(cnt0, cnt1)
}
}
t1 := f(rowMask, sameRow)
t2 := f(colMask, sameCol)
if t1 == -1 || t2 == -1 {
return -1
}
return t1 + t2
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|



