655. 输出二叉树

题目描述

给你一棵二叉树的根节点 root ，请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ，用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则：

• 树的 高度 为 height ，矩阵的行数 m 应该等于 height + 1 。
• 矩阵的列数 n 应该等于 2height+1 - 1 。
• 根节点 需要放置在 顶行 的 正中间 ，对应位置为 res[0][(n-1)/2] 。
• 对于放置在矩阵中的每个节点，设对应位置为 res[r][c] ，将其左子节点放置在 res[r+1][c-2height-r-1] ，右子节点放置在 res[r+1][c+2height-r-1] 。
• 继续这一过程，直到树中的所有节点都妥善放置。
• 任意空单元格都应该包含空字符串 "" 。

返回构造得到的矩阵 res 。

 

 

示例 1：

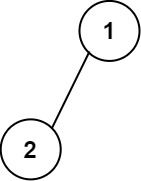
输入：root = [1,2]
输出：
[["","1",""],
 ["2","",""]]

示例 2：

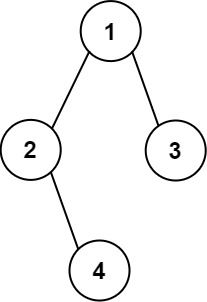
输入：root = [1,2,3,null,4]
输出：
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]

 

提示：

• 树中节点数在范围 [1, 210] 内
• -99 <= Node.val <= 99
• 树的深度在范围 [1, 10] 内

解法

方法一：两次 DFS

先通过 DFS 求二叉树的高度 $h$（高度从 0 开始），然后根据 $h$ 求得结果列表的行数 $m$ 和列数 $n$。

根据 $m$, $n$ 初始化结果列表 ans，然后 DFS 遍历二叉树，依次在每个位置填入二叉树节点值（字符串形式）即可。

时间复杂度 $O(h\times 2^h)$，空间复杂度 $O(h)$。其中 $h$ 是二叉树的高度。忽略结果返回值的空间消耗。

Python3JavaC++GoTypeScriptRust

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
        def height(root):
            if root is None:
                return -1
            return 1 + max(height(root.left), height(root.right))

        def dfs(root, r, c):
            if root is None:
                return
            ans[r][c] = str(root.val)
            dfs(root.left, r + 1, c - 2 ** (h - r - 1))
            dfs(root.right, r + 1, c + 2 ** (h - r - 1))

        h = height(root)
        m, n = h + 1, 2 ** (h + 1) - 1
        ans = [[""] * n for _ in range(m)]
        dfs(root, 0, (n - 1) // 2)
        return ans

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<String>> printTree(TreeNode root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        String[][] res = new String[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(res[i], "");
        }
        dfs(root, res, h, 0, (n - 1) / 2);
        List<List<String>> ans = new ArrayList<>();
        for (String[] t : res) {
            ans.add(Arrays.asList(t));
        }
        return ans;
    }

    private void dfs(TreeNode root, String[][] res, int h, int r, int c) {
        if (root == null) {
            return;
        }
        res[r][c] = String.valueOf(root.val);
        dfs(root.left, res, h, r + 1, c - (1 << (h - r - 1)));
        dfs(root.right, res, h, r + 1, c + (1 << (h - r - 1)));
    }

    private int height(TreeNode root) {
        if (root == null) {
            return -1;
        }
        return 1 + Math.max(height(root.left), height(root.right));
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<string>> printTree(TreeNode* root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        vector<vector<string>> ans(m, vector<string>(n, ""));
        dfs(root, ans, h, 0, (n - 1) / 2);
        return ans;
    }

    void dfs(TreeNode* root, vector<vector<string>>& ans, int h, int r, int c) {
        if (!root) return;
        ans[r][c] = to_string(root->val);
        dfs(root->left, ans, h, r + 1, c - pow(2, h - r - 1));
        dfs(root->right, ans, h, r + 1, c + pow(2, h - r - 1));
    }

    int height(TreeNode* root) {
        if (!root) return -1;
        return 1 + max(height(root->left), height(root->right));
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func printTree(root *TreeNode) [][]string {
    var height func(root *TreeNode) int
    height = func(root *TreeNode) int {
        if root == nil {
            return -1
        }
        return 1 + max(height(root.Left), height(root.Right))
    }
    h := height(root)
    m, n := h+1, (1<<(h+1))-1
    ans := make([][]string, m)
    for i := range ans {
        ans[i] = make([]string, n)
        for j := range ans[i] {
            ans[i][j] = ""
        }
    }
    var dfs func(root *TreeNode, r, c int)
    dfs = func(root *TreeNode, r, c int) {
        if root == nil {
            return
        }
        ans[r][c] = strconv.Itoa(root.Val)
        dfs(root.Left, r+1, c-int(math.Pow(float64(2), float64(h-r-1))))
        dfs(root.Right, r+1, c+int(math.Pow(float64(2), float64(h-r-1))))
    }

    dfs(root, 0, (n-1)/2)
    return ans
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function printTree(root: TreeNode | null): string[][] {
    const getHeight = (root: TreeNode | null, h: number) => {
        if (root == null) {
            return h - 1;
        }
        return Math.max(getHeight(root.left, h + 1), getHeight(root.right, h + 1));
    };

    const height = getHeight(root, 0);
    const m = height + 1;
    const n = 2 ** (height + 1) - 1;
    const res: string[][] = Array.from({ length: m }, () => new Array(n).fill(''));
    const dfs = (root: TreeNode | null, i: number, j: number) => {
        if (root === null) {
            return;
        }
        const { val, left, right } = root;
        res[i][j] = val + '';
        dfs(left, i + 1, j - 2 ** (height - i - 1));
        dfs(right, i + 1, j + 2 ** (height - i - 1));
    };
    dfs(root, 0, (n - 1) >>> 1);
    return res;
}

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    fn get_height(root: &Option<Rc<RefCell<TreeNode>>>, h: u32) -> u32 {
        if let Some(node) = root {
            let node = node.borrow();
            return Self::get_height(&node.left, h + 1).max(Self::get_height(&node.right, h + 1));
        }
        h - 1
    }

    fn dfs(
        root: &Option<Rc<RefCell<TreeNode>>>,
        i: usize,
        j: usize,
        res: &mut Vec<Vec<String>>,
        height: u32,
    ) {
        if root.is_none() {
            return;
        }
        let node = root.as_ref().unwrap().borrow();
        res[i][j] = node.val.to_string();
        Self::dfs(
            &node.left,
            i + 1,
            j - (2usize).pow(height - (i as u32) - 1),
            res,
            height,
        );
        Self::dfs(
            &node.right,
            i + 1,
            j + (2usize).pow(height - (i as u32) - 1),
            res,
            height,
        );
    }

    pub fn print_tree(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<Vec<String>> {
        let height = Self::get_height(&root, 0);
        let m = (height + 1) as usize;
        let n = (2usize).pow(height + 1) - 1;
        let mut res = vec![vec![String::new(); n]; m];
        Self::dfs(&root, 0, (n - 1) >> 1, &mut res, height);
        res
    }
}

方法二：两次 BFS

方法一中，我们是通过 DFS 来求二叉树的高度，我们也可以改成 BFS 的方式，逐层往下扩展，那么扩展的层数就是二叉树的高度。

同样，我们初始化结果列表 ans，然后 BFS 遍历二叉树，依次在每个位置填入二叉树节点值（字符串形式）即可。

时间复杂度 $O(h\times 2^h)$，空间复杂度 $O(h)$。其中 $h$ 是二叉树的高度。忽略结果返回值的空间消耗。

Python3JavaC++Go

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
        def height(root):
            q = deque([root])
            h = -1
            while q:
                h += 1
                for _ in range(len(q)):
                    root = q.popleft()
                    if root.left:
                        q.append(root.left)
                    if root.right:
                        q.append(root.right)
            return h

        h = height(root)
        m, n = h + 1, 2 ** (h + 1) - 1
        ans = [[""] * n for _ in range(m)]
        q = deque([(root, 0, (n - 1) // 2)])
        while q:
            node, r, c = q.popleft()
            ans[r][c] = str(node.val)
            if node.left:
                q.append((node.left, r + 1, c - 2 ** (h - r - 1)))
            if node.right:
                q.append((node.right, r + 1, c + 2 ** (h - r - 1)))
        return ans

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<String>> printTree(TreeNode root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        String[][] res = new String[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(res[i], "");
        }
        Deque<Tuple> q = new ArrayDeque<>();
        q.offer(new Tuple(root, 0, (n - 1) / 2));
        while (!q.isEmpty()) {
            Tuple p = q.pollFirst();
            root = p.node;
            int r = p.r, c = p.c;
            res[r][c] = String.valueOf(root.val);
            if (root.left != null) {
                q.offer(new Tuple(root.left, r + 1, c - (1 << (h - r - 1))));
            }
            if (root.right != null) {
                q.offer(new Tuple(root.right, r + 1, c + (1 << (h - r - 1))));
            }
        }
        List<List<String>> ans = new ArrayList<>();
        for (String[] t : res) {
            ans.add(Arrays.asList(t));
        }
        return ans;
    }

    private int height(TreeNode root) {
        Deque<TreeNode> q = new ArrayDeque<>();
        q.offer(root);
        int h = -1;
        while (!q.isEmpty()) {
            ++h;
            for (int n = q.size(); n > 0; --n) {
                root = q.pollFirst();
                if (root.left != null) {
                    q.offer(root.left);
                }
                if (root.right != null) {
                    q.offer(root.right);
                }
            }
        }
        return h;
    }
}

class Tuple {
    TreeNode node;
    int r;
    int c;

    public Tuple(TreeNode node, int r, int c) {
        this.node = node;
        this.r = r;
        this.c = c;
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<string>> printTree(TreeNode* root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        vector<vector<string>> ans(m, vector<string>(n, ""));
        queue<tuple<TreeNode*, int, int>> q;
        q.push({root, 0, (n - 1) / 2});
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            root = get<0>(p);
            int r = get<1>(p), c = get<2>(p);
            ans[r][c] = to_string(root->val);
            if (root->left) q.push({root->left, r + 1, c - pow(2, h - r - 1)});
            if (root->right) q.push({root->right, r + 1, c + pow(2, h - r - 1)});
        }
        return ans;
    }

    int height(TreeNode* root) {
        int h = -1;
        queue<TreeNode*> q{{root}};
        while (!q.empty()) {
            ++h;
            for (int n = q.size(); n; --n) {
                root = q.front();
                q.pop();
                if (root->left) q.push(root->left);
                if (root->right) q.push(root->right);
            }
        }
        return h;
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func printTree(root *TreeNode) [][]string {
    h := height(root)
    m, n := h+1, (1<<(h+1))-1
    ans := make([][]string, m)
    for i := range ans {
        ans[i] = make([]string, n)
        for j := range ans[i] {
            ans[i][j] = ""
        }
    }
    q := []tuple{tuple{root, 0, (n - 1) / 2}}
    for len(q) > 0 {
        p := q[0]
        q = q[1:]
        root := p.node
        r, c := p.r, p.c
        ans[r][c] = strconv.Itoa(root.Val)
        if root.Left != nil {
            q = append(q, tuple{root.Left, r + 1, c - int(math.Pow(float64(2), float64(h-r-1)))})
        }
        if root.Right != nil {
            q = append(q, tuple{root.Right, r + 1, c + int(math.Pow(float64(2), float64(h-r-1)))})
        }
    }
    return ans
}

func height(root *TreeNode) int {
    h := -1
    q := []*TreeNode{root}
    for len(q) > 0 {
        h++
        for n := len(q); n > 0; n-- {
            root := q[0]
            q = q[1:]
            if root.Left != nil {
                q = append(q, root.Left)
            }
            if root.Right != nil {
                q = append(q, root.Right)
            }
        }
    }
    return h
}

type tuple struct {
    node *TreeNode
    r    int
    c    int
}

评论