2673. 使二叉树所有路径值相等的最小代价

题目描述

给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中任意节点的值增加 1 。你可以执行操作任意次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回最少需要执行增加操作多少次。

注意：

满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个子节点，且所有叶子节点距离根节点距离相同。
路径值 指的是路径上所有节点的值之和。

示例 1：

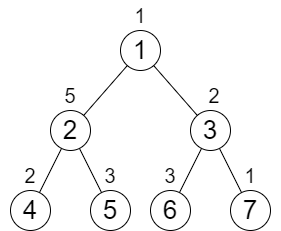
输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

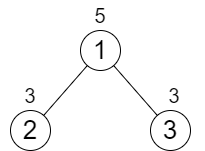
输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

提示：

3 <= n <= 10⁵
n + 1 是 2 的幂
cost.length == n
1 <= cost[i] <= 10⁴

解法

方法一：贪心

根据题目描述，我们需要计算最小的增加次数，使得根节点到每个叶子节点的路径值相等。

根节点到每个叶子节点的路径值相等，实际上等价于以任意节点为根节点的子树到该子树的每个叶子节点的路径值相等。

为什么呢？我们可以用反证法来证明。假设存在一个节点 $x$，以它为根节点的子树到某个叶子节点的路径值不相等，那么也就存在着根节点到叶子节点的路径值不相等的情况，这与“根节点到每个叶子节点的路径值相等”矛盾。因此假设不成立，以任意节点为根节点的子树到该子树的每个叶子节点的路径值相等。

我们可以从树的底部开始，逐层向上计算增加次数。对于每个非叶子节点，我们可以计算它的左右孩子节点的路径值，增加的次数为两者路径值的差值，然后将左右孩子节点的路径值更新为两者中的较大值。

最后返回总的增加的次数即可。

时间复杂度 $O(n)$，其中 $n$ 为节点数。空间复杂度 $O(1)$。

Python3JavaC++GoTypeScript

class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        ans = 0
        for i in range(n >> 1, 0, -1):
            l, r = i << 1, i << 1 | 1
            ans += abs(cost[l - 1] - cost[r - 1])
            cost[i - 1] += max(cost[l - 1], cost[r - 1])
        return ans

class Solution {
    public int minIncrements(int n, int[] cost) {
        int ans = 0;
        for (int i = n >> 1; i > 0; --i) {
            int l = i << 1, r = i << 1 | 1;
            ans += Math.abs(cost[l - 1] - cost[r - 1]);
            cost[i - 1] += Math.max(cost[l - 1], cost[r - 1]);
        }
        return ans;
    }
}

class Solution {
public:
    int minIncrements(int n, vector<int>& cost) {
        int ans = 0;
        for (int i = n >> 1; i > 0; --i) {
            int l = i << 1, r = i << 1 | 1;
            ans += abs(cost[l - 1] - cost[r - 1]);
            cost[i - 1] += max(cost[l - 1], cost[r - 1]);
        }
        return ans;
    }
};

func minIncrements(n int, cost []int) (ans int) {
    for i := n >> 1; i > 0; i-- {
        l, r := i<<1, i<<1|1
        ans += abs(cost[l-1] - cost[r-1])
        cost[i-1] += max(cost[l-1], cost[r-1])
    }
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

function minIncrements(n: number, cost: number[]): number {
    let ans = 0;
    for (let i = n >> 1; i; --i) {
        const [l, r] = [i << 1, (i << 1) | 1];
        ans += Math.abs(cost[l - 1] - cost[r - 1]);
        cost[i - 1] += Math.max(cost[l - 1], cost[r - 1]);
    }
    return ans;
}

2673. 使二叉树所有路径值相等的最小代价

题目描述

解法

方法一：贪心

评论