


题目描述
有一棵 n 个节点的无向树,节点编号为 0 到 n - 1 。
给你一个长度为 n 下标从 0 开始的整数数组 nums ,其中 nums[i] 表示第 i 个节点的值。同时给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 与 bi 之间有一条边。
你可以 删除 一些边,将这棵树分成几个连通块。一个连通块的 价值 定义为这个连通块中 所有 节点 i 对应的 nums[i] 之和。
你需要删除一些边,删除后得到的各个连通块的价值都相等。请返回你可以删除的边数 最多 为多少。
示例 1:
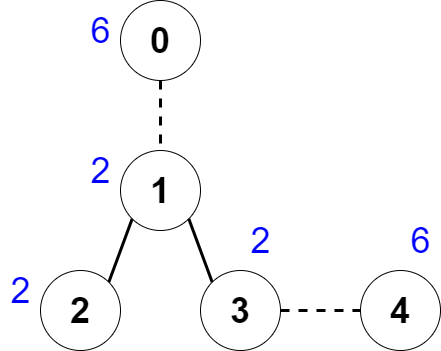
输入:nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]]
输出:2
解释:上图展示了我们可以删除边 [0,1] 和 [3,4] 。得到的连通块为 [0] ,[1,2,3] 和 [4] 。每个连通块的价值都为 6 。可以证明没有别的更好的删除方案存在了,所以答案为 2 。
示例 2:
输入:nums = [2], edges = []
输出:0
解释:没有任何边可以删除。
提示:
1 <= n <= 2 * 104nums.length == n1 <= nums[i] <= 50edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1edges 表示一棵合法的树。
解法
方法一:枚举连通块的个数
假设连通块的个数为 \(k\),那么要删除的边数为 \(k-1\),每个连通块的价值为 \(\frac{s}{k}\),其中 \(s\) 为 \(nums\) 所有节点的值之和。
我们从大到小枚举 \(k\),如果存在一个 \(k\),使得 \(\frac{s}{k}\) 是整数,并且得到的每个连通块的价值都相等,那么直接返回 \(k-1\)。其中 \(k\) 的初始值为 \(\min(n, \frac{s}{mx})\),记 \(mx\) 为 \(nums\) 中的最大值。
关键点在于判断对于给定的 \(\frac{s}{k}\),是否能划分出若干子树,使得每棵子树的价值都为 \(\frac{s}{k}\)。
这里我们通过 dfs 函数来判断,从上到下递归遍历求出各个子树的价值,如果子树价值和恰好为 \(\frac{s}{k}\),说明此时划分成功,我们将价值置为 \(0\) 返回给上一层,表示此子树可以与父节点断开。如果子树价值之和大于 \(\frac{s}{k}\),说明此时划分失败,我们返回 \(-1\),表示无法划分。
时间复杂度 \(O(n \times \sqrt{s})\),其中 \(n\) 和 \(s\) 分别为 \(nums\) 的长度和 \(nums\) 所有节点的值之和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution:
def componentValue(self, nums: List[int], edges: List[List[int]]) -> int:
def dfs(i, fa):
x = nums[i]
for j in g[i]:
if j != fa:
y = dfs(j, i)
if y == -1:
return -1
x += y
if x > t:
return -1
return x if x < t else 0
n = len(nums)
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
s = sum(nums)
mx = max(nums)
for k in range(min(n, s // mx), 1, -1):
if s % k == 0:
t = s // k
if dfs(0, -1) == 0:
return k - 1
return 0
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 | class Solution {
private List<Integer>[] g;
private int[] nums;
private int t;
public int componentValue(int[] nums, int[][] edges) {
int n = nums.length;
g = new List[n];
this.nums = nums;
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
int s = sum(nums), mx = max(nums);
for (int k = Math.min(n, s / mx); k > 1; --k) {
if (s % k == 0) {
t = s / k;
if (dfs(0, -1) == 0) {
return k - 1;
}
}
}
return 0;
}
private int dfs(int i, int fa) {
int x = nums[i];
for (int j : g[i]) {
if (j != fa) {
int y = dfs(j, i);
if (y == -1) {
return -1;
}
x += y;
}
}
if (x > t) {
return -1;
}
return x < t ? x : 0;
}
private int sum(int[] arr) {
int x = 0;
for (int v : arr) {
x += v;
}
return x;
}
private int max(int[] arr) {
int x = arr[0];
for (int v : arr) {
x = Math.max(x, v);
}
return x;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | class Solution {
public:
int componentValue(vector<int>& nums, vector<vector<int>>& edges) {
int n = nums.size();
int s = accumulate(nums.begin(), nums.end(), 0);
int mx = *max_element(nums.begin(), nums.end());
int t = 0;
unordered_map<int, vector<int>> g;
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
function<int(int, int)> dfs = [&](int i, int fa) -> int {
int x = nums[i];
for (int j : g[i]) {
if (j != fa) {
int y = dfs(j, i);
if (y == -1) return -1;
x += y;
}
}
if (x > t) return -1;
return x < t ? x : 0;
};
for (int k = min(n, s / mx); k > 1; --k) {
if (s % k == 0) {
t = s / k;
if (dfs(0, -1) == 0) {
return k - 1;
}
}
}
return 0;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 | func componentValue(nums []int, edges [][]int) int {
s, mx := 0, slices.Max(nums)
for _, x := range nums {
s += x
}
n := len(nums)
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
t := 0
var dfs func(int, int) int
dfs = func(i, fa int) int {
x := nums[i]
for _, j := range g[i] {
if j != fa {
y := dfs(j, i)
if y == -1 {
return -1
}
x += y
}
}
if x > t {
return -1
}
if x < t {
return x
}
return 0
}
for k := min(n, s/mx); k > 1; k-- {
if s%k == 0 {
t = s / k
if dfs(0, -1) == 0 {
return k - 1
}
}
}
return 0
}
|



