


题目描述
给你一个下标从 0 开始、大小为 m x n 的二进制矩阵 matrix ;另给你一个整数 numSelect,表示你必须从 matrix 中选择的 不同 列的数量。
如果一行中所有的 1 都被你选中的列所覆盖,则认为这一行被 覆盖 了。
形式上,假设 s = {c1, c2, ...., cnumSelect} 是你选择的列的集合。对于矩阵中的某一行 row ,如果满足下述条件,则认为这一行被集合 s 覆盖:
- 对于满足
matrix[row][col] == 1 的每个单元格 matrix[row][col](0 <= col <= n - 1),col 均存在于 s 中,或者
row 中 不存在 值为 1 的单元格。
你需要从矩阵中选出 numSelect 个列,使集合覆盖的行数最大化。
返回一个整数,表示可以由 numSelect 列构成的集合 覆盖 的 最大行数 。
示例 1:
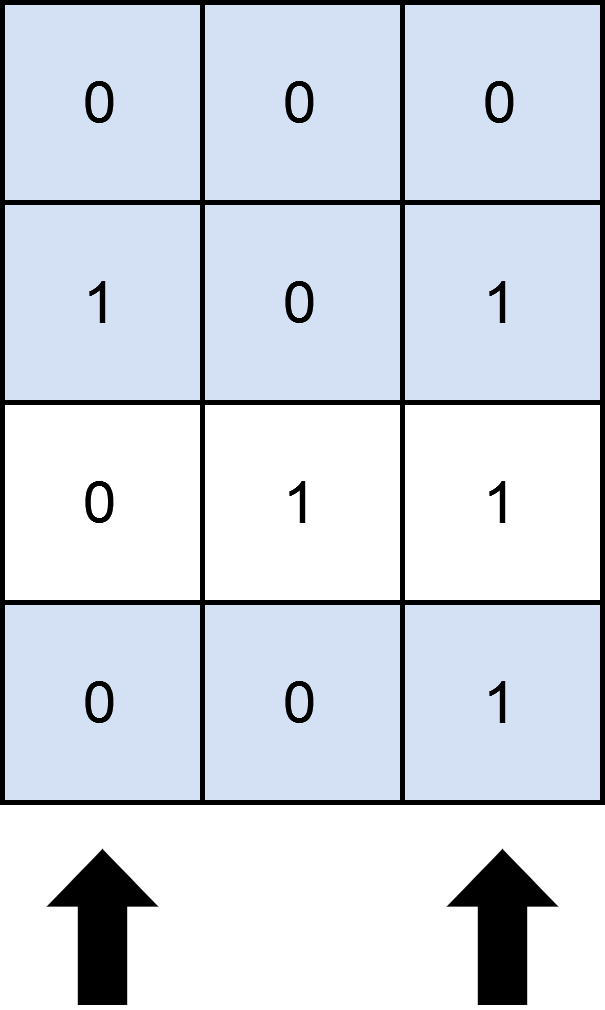
输入:matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
输出:3
解释:
图示中显示了一种覆盖 3 行的可行办法。
选择 s = {0, 2} 。
- 第 0 行被覆盖,因为其中没有出现 1 。
- 第 1 行被覆盖,因为值为 1 的两列(即 0 和 2)均存在于 s 中。
- 第 2 行未被覆盖,因为 matrix[2][1] == 1 但是 1 未存在于 s 中。
- 第 3 行被覆盖,因为 matrix[2][2] == 1 且 2 存在于 s 中。
因此,可以覆盖 3 行。
另外 s = {1, 2} 也可以覆盖 3 行,但可以证明无法覆盖更多行。
示例 2:

输入:matrix = [[1],[0]], numSelect = 1
输出:2
解释:
选择唯一的一列,两行都被覆盖了,因为整个矩阵都被覆盖了。
所以我们返回 2 。
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 12matrix[i][j] 要么是 0 要么是 11 <= numSelect <= n
解法
方法一:二进制枚举
我们先将矩阵中的每一行转换成一个二进制数,记录在数组 \(rows\) 中,其中 \(rows[i]\) 表示第 \(i\) 行对应的二进制数,而 \(rows[i]\) 这个二进制数的第 \(j\) 位表示第 \(i\) 行第 \(j\) 列的值。
接下来,我们枚举所有的 \(2^n\) 种列选择方案,其中 \(n\) 为矩阵的列数。对于每一种列选择方案,我们判断是否选中了 numSelect 列,如果不是,则跳过。否则,我们统计矩阵中有多少行中的所有 \(1\) 都被选中的列覆盖,即统计有多少行的二进制数 \(rows[i]\) 与列选择方案 \(mask\) 按位与的结果等于 \(rows[i]\),并更新最大的行数。
时间复杂度 \(O(2^n \times m)\),空间复杂度 \(O(m)\)。其中 \(m\) 和 \(n\) 分别为矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | class Solution:
def maximumRows(self, matrix: List[List[int]], numSelect: int) -> int:
rows = []
for row in matrix:
mask = reduce(or_, (1 << j for j, x in enumerate(row) if x), 0)
rows.append(mask)
ans = 0
for mask in range(1 << len(matrix[0])):
if mask.bit_count() != numSelect:
continue
t = sum((x & mask) == x for x in rows)
ans = max(ans, t)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public int maximumRows(int[][] matrix, int numSelect) {
int m = matrix.length, n = matrix[0].length;
int[] rows = new int[m];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == 1) {
rows[i] |= 1 << j;
}
}
}
int ans = 0;
for (int mask = 1; mask < 1 << n; ++mask) {
if (Integer.bitCount(mask) != numSelect) {
continue;
}
int t = 0;
for (int x : rows) {
if ((x & mask) == x) {
++t;
}
}
ans = Math.max(ans, t);
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public:
int maximumRows(vector<vector<int>>& matrix, int numSelect) {
int m = matrix.size(), n = matrix[0].size();
int rows[m];
memset(rows, 0, sizeof(rows));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j]) {
rows[i] |= 1 << j;
}
}
}
int ans = 0;
for (int mask = 1; mask < 1 << n; ++mask) {
if (__builtin_popcount(mask) != numSelect) {
continue;
}
int t = 0;
for (int x : rows) {
t += (x & mask) == x;
}
ans = max(ans, t);
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | func maximumRows(matrix [][]int, numSelect int) (ans int) {
m, n := len(matrix), len(matrix[0])
rows := make([]int, m)
for i, row := range matrix {
for j, x := range row {
if x == 1 {
rows[i] |= 1 << j
}
}
}
for mask := 1; mask < 1<<n; mask++ {
if bits.OnesCount(uint(mask)) != numSelect {
continue
}
t := 0
for _, x := range rows {
if (x & mask) == x {
t++
}
}
if ans < t {
ans = t
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | function maximumRows(matrix: number[][], numSelect: number): number {
const [m, n] = [matrix.length, matrix[0].length];
const rows: number[] = Array(m).fill(0);
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (matrix[i][j]) {
rows[i] |= 1 << j;
}
}
}
let ans = 0;
for (let mask = 1; mask < 1 << n; ++mask) {
if (bitCount(mask) !== numSelect) {
continue;
}
let t = 0;
for (const x of rows) {
if ((x & mask) === x) {
++t;
}
}
ans = Math.max(ans, t);
}
return ans;
}
function bitCount(i: number): number {
i = i - ((i >>> 1) & 0x55555555);
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
i = (i + (i >>> 4)) & 0x0f0f0f0f;
i = i + (i >>> 8);
i = i + (i >>> 16);
return i & 0x3f;
}
|




