跳转至

2374. 边积分最高的节点

题目描述

给你一个有向图，图中有 n 个节点，节点编号从 0 到 n - 1 ，其中每个节点都 恰有一条 出边。

图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示，其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。

节点 i 的 边积分 定义为：所有存在一条指向节点 i 的边的节点的 编号 总和。

返回 边积分 最高的节点。如果多个节点的 边积分 相同，返回编号 最小 的那个。

 

示例 1：

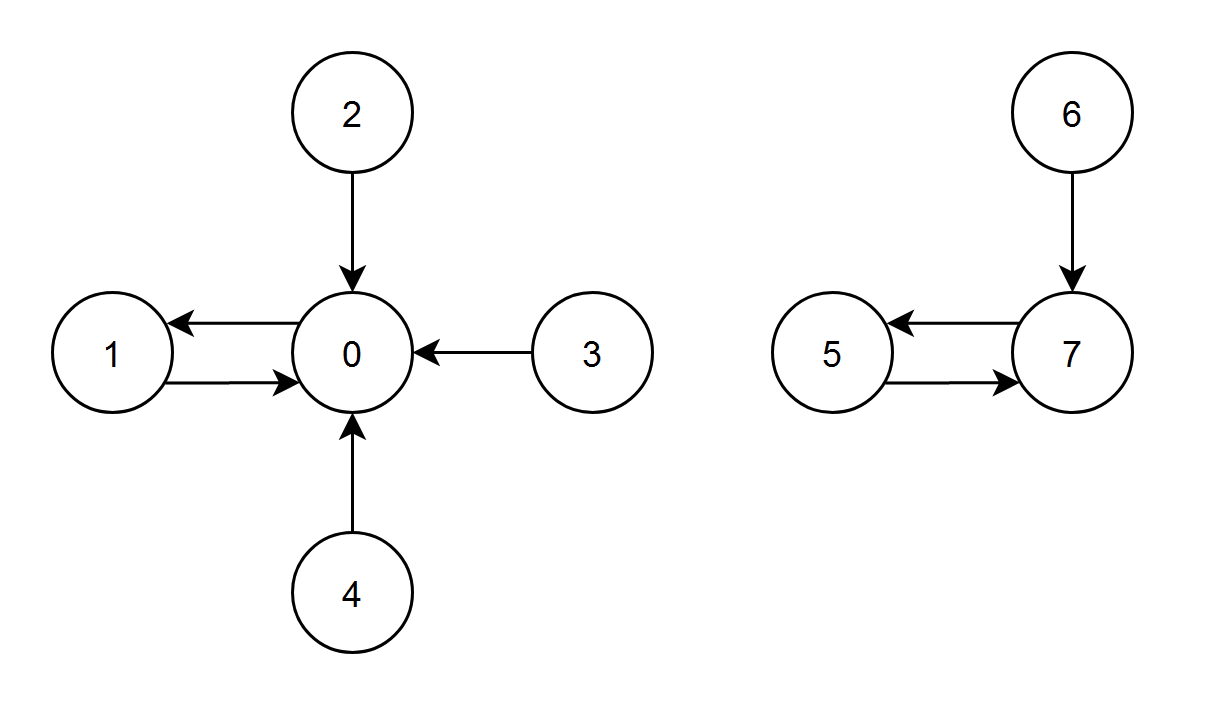
输入：edges = [1,0,0,0,0,7,7,5]
输出：7
解释：
- 节点 1、2、3 和 4 都有指向节点 0 的边，节点 0 的边积分等于 1 + 2 + 3 + 4 = 10 。
- 节点 0 有一条指向节点 1 的边，节点 1 的边积分等于 0 。
- 节点 7 有一条指向节点 5 的边，节点 5 的边积分等于 7 。
- 节点 5 和 6 都有指向节点 7 的边，节点 7 的边积分等于 5 + 6 = 11 。
节点 7 的边积分最高，所以返回 7 。

示例 2：

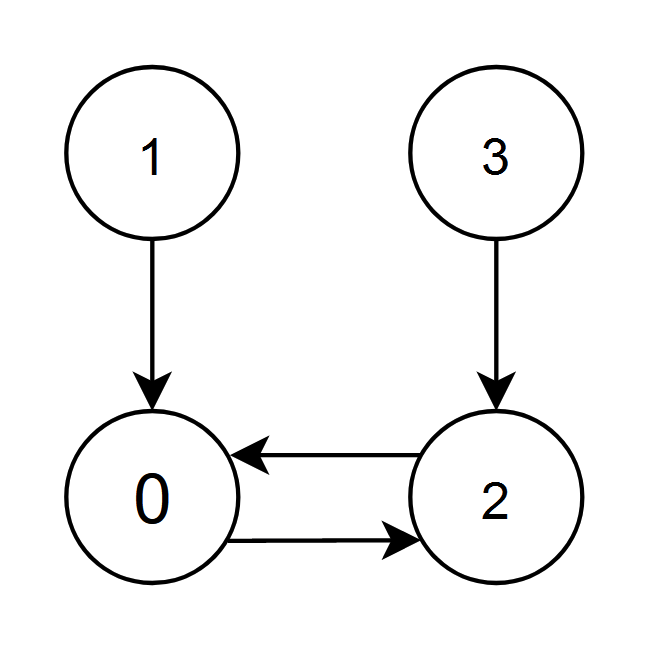
输入：edges = [2,0,0,2]
输出：0
解释：
- 节点 1 和 2 都有指向节点 0 的边，节点 0 的边积分等于 1 + 2 = 3 。
- 节点 0 和 3 都有指向节点 2 的边，节点 2 的边积分等于 0 + 3 = 3 。
节点 0 和 2 的边积分都是 3 。由于节点 0 的编号更小，返回 0 。

 

提示：

  • n == edges.length
  • 2 <= n <= 105
  • 0 <= edges[i] < n
  • edges[i] != i

解法

方法一：一次遍历

我们定义一个长度为 $n$ 的数组 $\textit{cnt}$，其中 $\textit{cnt}[i]$ 表示节点 $i$ 的边积分，初始时所有元素均为 $0$。定义一个答案变量 $\textit{ans}$，初始时为 $0$。

接下来，我们遍历数组 $\textit{edges}$，对于每个节点 $i$，以及它的出边节点 $j$，我们更新 $\textit{cnt}[j]$ 为 $\textit{cnt}[j] + i$。如果 $\textit{cnt}[\textit{ans}] < \textit{cnt}[j]$ 或者 $\textit{cnt}[\textit{ans}] = \textit{cnt}[j]$ 且 $j < \textit{ans}$，我们更新 $\textit{ans}$ 为 $j$。

最后，返回 $\textit{ans}$ 即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为数组 $\textit{edges}$ 的长度。

1
2
3
4
5
6
7
8
9
class Solution:
    def edgeScore(self, edges: List[int]) -> int:
        ans = 0
        cnt = [0] * len(edges)
        for i, j in enumerate(edges):
            cnt[j] += i
            if cnt[ans] < cnt[j] or (cnt[ans] == cnt[j] and j < ans):
                ans = j
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
    public int edgeScore(int[] edges) {
        int n = edges.length;
        long[] cnt = new long[n];
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int j = edges[i];
            cnt[j] += i;
            if (cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans)) {
                ans = j;
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
public:
    int edgeScore(vector<int>& edges) {
        int n = edges.size();
        vector<long long> cnt(n);
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int j = edges[i];
            cnt[j] += i;
            if (cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans)) {
                ans = j;
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
func edgeScore(edges []int) (ans int) {
    cnt := make([]int, len(edges))
    for i, j := range edges {
        cnt[j] += i
        if cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans) {
            ans = j
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
function edgeScore(edges: number[]): number {
    const n = edges.length;
    const cnt: number[] = Array(n).fill(0);
    let ans: number = 0;
    for (let i = 0; i < n; ++i) {
        const j = edges[i];
        cnt[j] += i;
        if (cnt[ans] < cnt[j] || (cnt[ans] === cnt[j] && j < ans)) {
            ans = j;
        }
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
impl Solution {
    pub fn edge_score(edges: Vec<i32>) -> i32 {
        let n = edges.len();
        let mut cnt = vec![0_i64; n];
        let mut ans = 0;

        for (i, &j) in edges.iter().enumerate() {
            let j = j as usize;
            cnt[j] += i as i64;
            if cnt[ans] < cnt[j] || (cnt[ans] == cnt[j] && j < ans) {
                ans = j;
            }
        }

        ans as i32
    }
}

评论