
题目描述
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。
给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
示例 1:
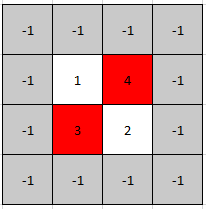
输入: mat = [[1,4],[3,2]]
输出: [0,1]
解释: 3 和 4 都是峰值,所以[1,0]和[0,1]都是可接受的答案。
示例 2:
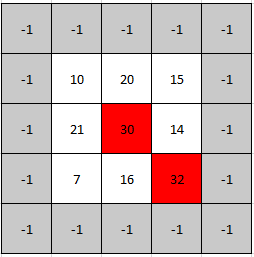
输入: mat = [[10,20,15],[21,30,14],[7,16,32]]
输出: [1,1]
解释: 30 和 32 都是峰值,所以[1,1]和[2,2]都是可接受的答案。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 105- 任意两个相邻元素均不相等.
解法
方法一:二分查找
记 \(m\) 和 \(n\) 分别为矩阵的行数和列数。
题目要求我们寻找峰值,并且时间复杂度为 \(O(m \times \log n)\) 或 \(O(n \times \log m)\),那么我们可以考虑使用二分查找。
我们考虑第 \(i\) 行的最大值,不妨将其下标记为 \(j\)。
如果 \(mat[i][j] \gt mat[i + 1][j]\),那么第 \([0,..i]\) 行中必然存在一个峰值,我们只需要在第 \([0,..i]\) 行中找到最大值即可。同理,如果 \(mat[i][j] \lt mat[i + 1][j]\),那么第 \([i + 1,..m - 1]\) 行中必然存在一个峰值,我们只需要在第 \([i + 1,..m - 1]\) 行中找到最大值即可。
为什么上述做法是对的?我们不妨用反证法来证明。
如果 \(mat[i][j] \gt mat[i + 1][j]\),假设第 \([0,..i]\) 行中不存在峰值,那么 \(mat[i][j]\) 不是峰值,而由于 \(mat[i][j]\) 是第 \(i\) 行的最大值,并且 \(mat[i][j] \gt mat[i + 1][j]\),那么 \(mat[i][j] \lt mat[i - 1][j]\)。我们继续从第 \(i - 1\) 行往上考虑,每一行的最大值都小于上一行的最大值。那么当遍历到 \(i = 0\) 时,由于矩阵中的元素都是正整数,并且矩阵周边一圈的格子的值都为 \(-1\)。因此,在第 \(0\) 行时,其最大值大于其所有相邻元素,那么第 \(0\) 行的最大值就是峰值,与假设矛盾。因此,第 \([0,..i]\) 行中必然存在一个峰值。
对于 \(mat[i][j] \lt mat[i + 1][j]\) 的情况,我们可以用类似的方法证明第 \([i + 1,..m - 1]\) 行中必然存在一个峰值。
因此,我们可以使用二分查找来寻找峰值。
我们二分查找矩阵的行,初始时查找的边界为 \(l = 0\), \(r = m - 1\)。每一次,我们找到当前的中间行 \(mid\),并找到该行的最大值下标 \(j\)。如果 \(mat[mid][j] \gt mat[mid + 1][j]\),那么我们就在第 \([0,..mid]\) 行中寻找峰值,即更新 \(r = mid\)。否则,我们就在第 \([mid + 1,..m - 1]\) 行中寻找峰值,即更新 \(l = mid + 1\)。当 \(l = r\) 时,我们就找到了峰值所在的位置 \([l, j_l]\)。其中 \(j_l\) 是第 \(l\) 行的最大值下标。
时间复杂度 \(O(n \times \log m)\),其中 \(m\) 和 \(n\) 分别为矩阵的行数和列数。二分查找的时间复杂度为 \(O(\log m)\),每次二分查找时,我们需要遍历第 \(mid\) 行的所有元素,时间复杂度为 \(O(n)\)。空间复杂度 \(O(1)\)。
| class Solution:
def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
l, r = 0, len(mat) - 1
while l < r:
mid = (l + r) >> 1
j = mat[mid].index(max(mat[mid]))
if mat[mid][j] > mat[mid + 1][j]:
r = mid
else:
l = mid + 1
return [l, mat[l].index(max(mat[l]))]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution {
public int[] findPeakGrid(int[][] mat) {
int l = 0, r = mat.length - 1;
int n = mat[0].length;
while (l < r) {
int mid = (l + r) >> 1;
int j = maxPos(mat[mid]);
if (mat[mid][j] > mat[mid + 1][j]) {
r = mid;
} else {
l = mid + 1;
}
}
return new int[] {l, maxPos(mat[l])};
}
private int maxPos(int[] arr) {
int j = 0;
for (int i = 1; i < arr.length; ++i) {
if (arr[j] < arr[i]) {
j = i;
}
}
return j;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public:
vector<int> findPeakGrid(vector<vector<int>>& mat) {
int l = 0, r = mat.size() - 1;
while (l < r) {
int mid = (l + r) >> 1;
int j = distance(mat[mid].begin(), max_element(mat[mid].begin(), mat[mid].end()));
if (mat[mid][j] > mat[mid + 1][j]) {
r = mid;
} else {
l = mid + 1;
}
}
int j = distance(mat[l].begin(), max_element(mat[l].begin(), mat[l].end()));
return {l, j};
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | func findPeakGrid(mat [][]int) []int {
maxPos := func(arr []int) int {
j := 0
for i := 1; i < len(arr); i++ {
if arr[i] > arr[j] {
j = i
}
}
return j
}
l, r := 0, len(mat)-1
for l < r {
mid := (l + r) >> 1
j := maxPos(mat[mid])
if mat[mid][j] > mat[mid+1][j] {
r = mid
} else {
l = mid + 1
}
}
return []int{l, maxPos(mat[l])}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13 | function findPeakGrid(mat: number[][]): number[] {
let [l, r] = [0, mat.length - 1];
while (l < r) {
const mid = (l + r) >> 1;
const j = mat[mid].indexOf(Math.max(...mat[mid]));
if (mat[mid][j] > mat[mid + 1][j]) {
r = mid;
} else {
l = mid + 1;
}
}
return [l, mat[l].indexOf(Math.max(...mat[l]))];
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | impl Solution {
pub fn find_peak_grid(mat: Vec<Vec<i32>>) -> Vec<i32> {
let mut l: usize = 0;
let mut r: usize = mat.len() - 1;
while l < r {
let mid: usize = (l + r) >> 1;
let j: usize = mat[mid]
.iter()
.position(|&x| x == *mat[mid].iter().max().unwrap())
.unwrap();
if mat[mid][j] > mat[mid + 1][j] {
r = mid;
} else {
l = mid + 1;
}
}
let j: usize = mat[l]
.iter()
.position(|&x| x == *mat[l].iter().max().unwrap())
.unwrap();
vec![l as i32, j as i32]
}
}
|


