


题目描述
给你一个 n 个节点的树(也就是一个无环连通无向图),节点编号从 0 到 n - 1 ,且恰好有 n - 1 条边,每个节点有一个值。树的 根节点 为 0 号点。
给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值,edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。
当 gcd(x, y) == 1 ,我们称两个数 x 和 y 是 互质的 ,其中 gcd(x, y) 是 x 和 y 的 最大公约数 。
从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。
请你返回一个大小为 n 的数组 ans ,其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ,如果不存在这样的祖先节点,ans[i] 为 -1 。
示例 1:
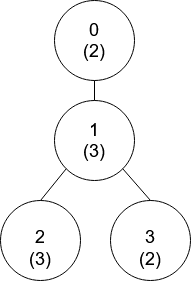
输入:nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出:[-1,0,0,1]
解释:上图中,每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的(gcd(2,3) == 1)。
- 节点 2 有两个祖先节点,分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的(gcd(3,3) == 3)但节点 0 的值是互质的(gcd(2,3) == 1),所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点,分别是节点 1 和节点 0 。它与节点 1 互质(gcd(3,2) == 1),所以节点 1 是离它最近的符合要求的祖先节点。
示例 2:
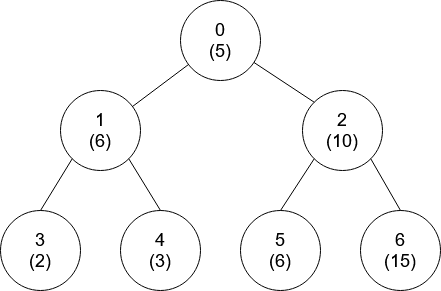
输入:nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出:[-1,0,-1,0,0,0,-1]
提示:
nums.length == n1 <= nums[i] <= 501 <= n <= 105edges.length == n - 1edges[j].length == 20 <= uj, vj < nuj != vj
解法
方法一:预处理 + 枚举 + 栈 + 回溯
由于题目中 \(nums[i]\) 的取值范围为 \([1, 50]\),因此我们可以预处理出每个数的所有互质数,记录在数组 \(f\) 中,其中 \(f[i]\) 表示 \(i\) 的所有互质数。
接下来我们可以使用回溯的方法,从根节点开始遍历整棵树,对于每个节点 \(i\),我们可以通过 \(f\) 数组得到 \(nums[i]\) 的所有互质数。然后我们枚举 \(nums[i]\) 的所有互质数,找到已经出现过的且深度最大的祖先节点 \(t\),即为 \(i\) 的最近的互质祖先节点。这里我们可以用一个长度为 \(51\) 的栈数组 \(stks\) 来获取每个出现过的值 \(v\) 的节点以及其深度。每个栈 \(stks[v]\) 的栈顶元素就是最近的深度最大的祖先节点。
时间复杂度 \(O(n \times M)\),空间复杂度 \(O(M^2 + n)\)。其中 \(n\) 为节点个数,而 \(M\) 为 \(nums[i]\) 的最大值,本题中 \(M = 50\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | class Solution:
def getCoprimes(self, nums: List[int], edges: List[List[int]]) -> List[int]:
def dfs(i, fa, depth):
t = k = -1
for v in f[nums[i]]:
stk = stks[v]
if stk and stk[-1][1] > k:
t, k = stk[-1]
ans[i] = t
for j in g[i]:
if j != fa:
stks[nums[i]].append((i, depth))
dfs(j, i, depth + 1)
stks[nums[i]].pop()
g = defaultdict(list)
for u, v in edges:
g[u].append(v)
g[v].append(u)
f = defaultdict(list)
for i in range(1, 51):
for j in range(1, 51):
if gcd(i, j) == 1:
f[i].append(j)
stks = defaultdict(list)
ans = [-1] * len(nums)
dfs(0, -1, 0)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 | class Solution {
private List<Integer>[] g;
private List<Integer>[] f;
private Deque<int[]>[] stks;
private int[] nums;
private int[] ans;
public int[] getCoprimes(int[] nums, int[][] edges) {
int n = nums.length;
g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : edges) {
int u = e[0], v = e[1];
g[u].add(v);
g[v].add(u);
}
f = new List[51];
stks = new Deque[51];
Arrays.setAll(f, k -> new ArrayList<>());
Arrays.setAll(stks, k -> new ArrayDeque<>());
for (int i = 1; i < 51; ++i) {
for (int j = 1; j < 51; ++j) {
if (gcd(i, j) == 1) {
f[i].add(j);
}
}
}
this.nums = nums;
ans = new int[n];
dfs(0, -1, 0);
return ans;
}
private void dfs(int i, int fa, int depth) {
int t = -1, k = -1;
for (int v : f[nums[i]]) {
var stk = stks[v];
if (!stk.isEmpty() && stk.peek()[1] > k) {
t = stk.peek()[0];
k = stk.peek()[1];
}
}
ans[i] = t;
for (int j : g[i]) {
if (j != fa) {
stks[nums[i]].push(new int[] {i, depth});
dfs(j, i, depth + 1);
stks[nums[i]].pop();
}
}
}
private int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | class Solution {
public:
vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) {
int n = nums.size();
vector<vector<int>> g(n);
vector<vector<int>> f(51);
vector<stack<pair<int, int>>> stks(51);
for (auto& e : edges) {
int u = e[0], v = e[1];
g[u].emplace_back(v);
g[v].emplace_back(u);
}
for (int i = 1; i < 51; ++i) {
for (int j = 1; j < 51; ++j) {
if (__gcd(i, j) == 1) {
f[i].emplace_back(j);
}
}
}
vector<int> ans(n);
function<void(int, int, int)> dfs = [&](int i, int fa, int depth) {
int t = -1, k = -1;
for (int v : f[nums[i]]) {
auto& stk = stks[v];
if (!stk.empty() && stk.top().second > k) {
t = stk.top().first;
k = stk.top().second;
}
}
ans[i] = t;
for (int j : g[i]) {
if (j != fa) {
stks[nums[i]].push({i, depth});
dfs(j, i, depth + 1);
stks[nums[i]].pop();
}
}
};
dfs(0, -1, 0);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | func getCoprimes(nums []int, edges [][]int) []int {
n := len(nums)
g := make([][]int, n)
f := [51][]int{}
type pair struct{ first, second int }
stks := [51][]pair{}
for _, e := range edges {
u, v := e[0], e[1]
g[u] = append(g[u], v)
g[v] = append(g[v], u)
}
for i := 1; i < 51; i++ {
for j := 1; j < 51; j++ {
if gcd(i, j) == 1 {
f[i] = append(f[i], j)
}
}
}
ans := make([]int, n)
var dfs func(i, fa, depth int)
dfs = func(i, fa, depth int) {
t, k := -1, -1
for _, v := range f[nums[i]] {
stk := stks[v]
if len(stk) > 0 && stk[len(stk)-1].second > k {
t, k = stk[len(stk)-1].first, stk[len(stk)-1].second
}
}
ans[i] = t
for _, j := range g[i] {
if j != fa {
stks[nums[i]] = append(stks[nums[i]], pair{i, depth})
dfs(j, i, depth+1)
stks[nums[i]] = stks[nums[i]][:len(stks[nums[i]])-1]
}
}
}
dfs(0, -1, 0)
return ans
}
func gcd(a, b int) int {
if b == 0 {
return a
}
return gcd(b, a%b)
}
|




