


题目描述
给定一个 m x n 的二进制矩阵 mat,返回矩阵 mat 中特殊位置的数量。
如果位置 (i, j) 满足 mat[i][j] == 1 并且行 i 与列 j 中的所有其他元素都是 0(行和列的下标从 0 开始计数),那么它被称为 特殊 位置。
示例 1:
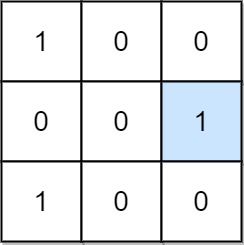
输入:mat = [[1,0,0],[0,0,1],[1,0,0]]
输出:1
解释:位置 (1, 2) 是一个特殊位置,因为 mat[1][2] == 1 且第 1 行和第 2 列的其他所有元素都是 0。
示例 2:
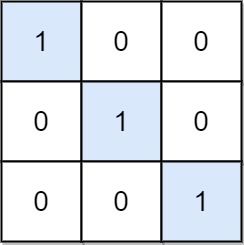
输入:mat = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
解释:位置 (0, 0),(1, 1) 和 (2, 2) 都是特殊位置。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 100mat[i][j] 是 0 或 1。
解法
方法一:计数
我们可以用两个数组 \(\textit{rows}\) 和 \(\textit{cols}\) 分别记录每一行和每一列的 \(1\) 的个数。
然后遍历矩阵,对于每一个 \(1\),检查其所在的行和列是否只有一个 \(1\),如果是则答案加一。
遍历结束后,返回答案即可。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(m + n)\)。其中 \(m\) 和 \(n\) 分别是矩阵 \(\textit{mat}\) 的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13 | class Solution:
def numSpecial(self, mat: List[List[int]]) -> int:
rows = [0] * len(mat)
cols = [0] * len(mat[0])
for i, row in enumerate(mat):
for j, x in enumerate(row):
rows[i] += x
cols[j] += x
ans = 0
for i, row in enumerate(mat):
for j, x in enumerate(row):
ans += x == 1 and rows[i] == 1 and cols[j] == 1
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | class Solution {
public int numSpecial(int[][] mat) {
int m = mat.length, n = mat[0].length;
int[] rows = new int[m];
int[] cols = new int[n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
rows[i] += mat[i][j];
cols[j] += mat[i][j];
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1) {
ans++;
}
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution {
public:
int numSpecial(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
vector<int> rows(m);
vector<int> cols(n);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
rows[i] += mat[i][j];
cols[j] += mat[i][j];
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1) {
ans++;
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | func numSpecial(mat [][]int) (ans int) {
rows := make([]int, len(mat))
cols := make([]int, len(mat[0]))
for i, row := range mat {
for j, x := range row {
rows[i] += x
cols[j] += x
}
}
for i, row := range mat {
for j, x := range row {
if x == 1 && rows[i] == 1 && cols[j] == 1 {
ans++
}
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | function numSpecial(mat: number[][]): number {
const m = mat.length;
const n = mat[0].length;
const rows: number[] = Array(m).fill(0);
const cols: number[] = Array(n).fill(0);
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
rows[i] += mat[i][j];
cols[j] += mat[i][j];
}
}
let ans = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (mat[i][j] === 1 && rows[i] === 1 && cols[j] === 1) {
++ans;
}
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | impl Solution {
pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {
let m = mat.len();
let n = mat[0].len();
let mut rows = vec![0; m];
let mut cols = vec![0; n];
for i in 0..m {
for j in 0..n {
rows[i] += mat[i][j];
cols[j] += mat[i][j];
}
}
let mut ans = 0;
for i in 0..m {
for j in 0..n {
if mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1 {
ans += 1;
}
}
}
ans
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | int numSpecial(int** mat, int matSize, int* matColSize) {
int m = matSize, n = matColSize[0];
int rows[m];
int cols[n];
memset(rows, 0, sizeof(rows));
memset(cols, 0, sizeof(cols));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
rows[i] += mat[i][j];
cols[j] += mat[i][j];
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1) {
ans++;
}
}
}
return ans;
}
|




