


题目描述
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
示例 1:
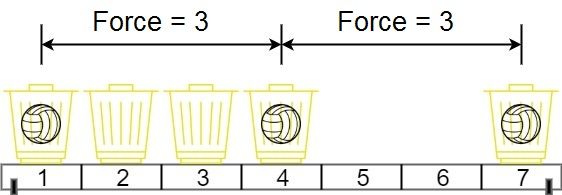
输入:position = [1,2,3,4,7], m = 3
输出:3
解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。
示例 2:
输入:position = [5,4,3,2,1,1000000000], m = 2
输出:999999999
解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
提示:
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- 所有
position 中的整数 互不相同 。
2 <= m <= position.length
解法
方法一:二分查找
我们注意到,任意两球间的最小磁力越大,能够放入的球的数量就越少,这存在着单调性。我们可以使用二分查找,找到最大的最小磁力,使得能够放入的球的数量不小于 \(m\)。
我们首先对篮子的位置进行排序,然后使用二分查找的方法,定义二分查找的左边界 \(l = 1\),右边界 \(r = \textit{position}[n - 1]\),其中 \(n\) 为篮子的数量。在每次二分查找的过程中,我们计算取中值 \(m = (l + r + 1) / 2\),然后判断是否存在一种放置球的方法,使得能够放入的球的数量不小于 \(m\)。
问题转换为判断一个给定的最小磁力 \(f\) 是否能够放入 \(m\) 个球。我们可以从左到右遍历篮子的位置,如果上一个球的位置与当前篮子的位置的距离大于等于 \(f\),则说明可以在当前篮子放置一个球。最后判断放置的球的数量是否不小于 \(m\) 即可。
时间复杂度 \(O(n \times \log n + n \times \log M)\),空间复杂度 \(O(\log n)\)。其中 \(n\) 和 \(M\) 分别为篮子的数量和篮子的位置的最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | class Solution:
def maxDistance(self, position: List[int], m: int) -> int:
def check(f: int) -> bool:
prev = -inf
cnt = 0
for curr in position:
if curr - prev >= f:
prev = curr
cnt += 1
return cnt < m
position.sort()
l, r = 1, position[-1]
return bisect_left(range(l, r + 1), True, key=check)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | class Solution {
private int[] position;
public int maxDistance(int[] position, int m) {
Arrays.sort(position);
this.position = position;
int l = 1, r = position[position.length - 1];
while (l < r) {
int mid = (l + r + 1) >> 1;
if (count(mid) >= m) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
private int count(int f) {
int prev = position[0];
int cnt = 1;
for (int curr : position) {
if (curr - prev >= f) {
++cnt;
prev = curr;
}
}
return cnt;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public:
int maxDistance(vector<int>& position, int m) {
ranges::sort(position);
int l = 1, r = position.back();
auto count = [&](int f) {
int prev = position[0];
int cnt = 1;
for (int& curr : position) {
if (curr - prev >= f) {
prev = curr;
cnt++;
}
}
return cnt;
};
while (l < r) {
int mid = (l + r + 1) >> 1;
if (count(mid) >= m) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | func maxDistance(position []int, m int) int {
sort.Ints(position)
return sort.Search(position[len(position)-1], func(f int) bool {
prev := position[0]
cnt := 1
for _, curr := range position {
if curr-prev >= f {
cnt++
prev = curr
}
}
return cnt < m
}) - 1
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | function maxDistance(position: number[], m: number): number {
position.sort((a, b) => a - b);
let [l, r] = [1, position.at(-1)!];
const count = (f: number): number => {
let cnt = 1;
let prev = position[0];
for (const curr of position) {
if (curr - prev >= f) {
cnt++;
prev = curr;
}
}
return cnt;
};
while (l < r) {
const mid = (l + r + 1) >> 1;
if (count(mid) >= m) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | /**
* @param {number[]} position
* @param {number} m
* @return {number}
*/
var maxDistance = function (position, m) {
position.sort((a, b) => a - b);
let [l, r] = [1, position.at(-1)];
const count = f => {
let cnt = 1;
let prev = position[0];
for (const curr of position) {
if (curr - prev >= f) {
cnt++;
prev = curr;
}
}
return cnt;
};
while (l < r) {
const mid = (l + r + 1) >> 1;
if (count(mid) >= m) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
};
|



