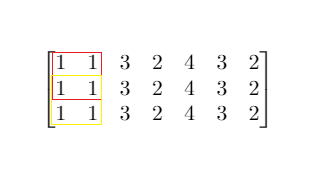题目描述
给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。
请你返回元素总和小于或等于阈值的正方形区域的最大边长;如果没有这样的正方形区域,则返回 0 。
示例 1:
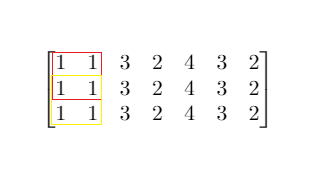
输入:mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出:2
解释:总和小于或等于 4 的正方形的最大边长为 2,如图所示。
示例 2:
输入:mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出:0
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 3000 <= mat[i][j] <= 1040 <= threshold <= 105
解法
方法一:二维前缀和 + 二分查找
我们可以先预处理得到二维前缀和数组 \(s\),其中 \(s[i + 1][j + 1]\) 表示矩阵 \(mat\) 中从 \((0, 0)\) 到 \((i, j)\) 的元素和,那么对于任意的正方形区域,我们都可以在 \(O(1)\) 的时间内得到其元素和。
接下来,我们可以使用二分查找的方法得到最大的边长。我们枚举正方形的边长 \(k\),然后枚举正方形的左上角位置 \((i, j)\),那么我们可以得到正方形的元素和 \(v\),如果 \(v \leq threshold\),那么说明存在边长为 \(k\) 的正方形区域的元素和小于或等于阈值,否则不存在。
时间复杂度 \(O(m \times n \times \log \min(m, n))\),空间复杂度 \(O(m \times n)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution:
def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
def check(k: int) -> bool:
for i in range(m - k + 1):
for j in range(n - k + 1):
v = s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j]
if v <= threshold:
return True
return False
m, n = len(mat), len(mat[0])
s = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(mat, 1):
for j, x in enumerate(row, 1):
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x
l, r = 0, min(m, n)
while l < r:
mid = (l + r + 1) >> 1
if check(mid):
l = mid
else:
r = mid - 1
return l
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | class Solution {
private int m;
private int n;
private int threshold;
private int[][] s;
public int maxSideLength(int[][] mat, int threshold) {
m = mat.length;
n = mat[0].length;
this.threshold = threshold;
s = new int[m + 1][n + 1];
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
int l = 0, r = Math.min(m, n);
while (l < r) {
int mid = (l + r + 1) >> 1;
if (check(mid)) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
private boolean check(int k) {
for (int i = 0; i < m - k + 1; ++i) {
for (int j = 0; j < n - k + 1; ++j) {
if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
return true;
}
}
}
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution {
public:
int maxSideLength(vector<vector<int>>& mat, int threshold) {
int m = mat.size(), n = mat[0].size();
int s[m + 1][n + 1];
memset(s, 0, sizeof(s));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
auto check = [&](int k) {
for (int i = 0; i < m - k + 1; ++i) {
for (int j = 0; j < n - k + 1; ++j) {
if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
return true;
}
}
}
return false;
};
int l = 0, r = min(m, n);
while (l < r) {
int mid = (l + r + 1) >> 1;
if (check(mid)) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | func maxSideLength(mat [][]int, threshold int) int {
m, n := len(mat), len(mat[0])
s := make([][]int, m+1)
for i := range s {
s[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + mat[i-1][j-1]
}
}
check := func(k int) bool {
for i := 0; i < m-k+1; i++ {
for j := 0; j < n-k+1; j++ {
if s[i+k][j+k]-s[i][j+k]-s[i+k][j]+s[i][j] <= threshold {
return true
}
}
}
return false
}
l, r := 0, min(m, n)
for l < r {
mid := (l + r + 1) >> 1
if check(mid) {
l = mid
} else {
r = mid - 1
}
}
return l
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | function maxSideLength(mat: number[][], threshold: number): number {
const m = mat.length;
const n = mat[0].length;
const s: number[][] = Array(m + 1)
.fill(0)
.map(() => Array(n + 1).fill(0));
for (let i = 1; i <= m; ++i) {
for (let j = 1; j <= n; ++j) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
const check = (k: number): boolean => {
for (let i = 0; i < m - k + 1; ++i) {
for (let j = 0; j < n - k + 1; ++j) {
if (s[i + k][j + k] - s[i + k][j] - s[i][j + k] + s[i][j] <= threshold) {
return true;
}
}
}
return false;
};
let l = 0;
let r = Math.min(m, n);
while (l < r) {
const mid = (l + r + 1) >> 1;
if (check(mid)) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
|