
题目描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
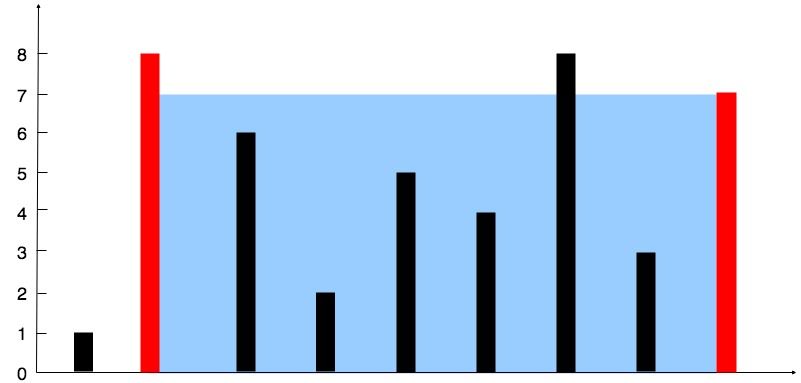
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
解法
方法一:双指针
我们使用两个指针 \(l\) 和 \(r\) 分别指向数组的左右两端,即 \(l = 0\),而 \(r = n - 1\),其中 \(n\) 是数组的长度。
接下来,我们使用变量 \(\textit{ans}\) 记录容器的最大容量,初始化为 \(0\)。
然后,我们开始进行循环,每次循环中,我们计算当前容器的容量,即 \(\textit{min}(height[l], height[r]) \times (r - l)\),并将其与 \(\textit{ans}\) 进行比较,将较大值赋给 \(\textit{ans}\)。然后,我们判断 \(height[l]\) 和 \(height[r]\) 的大小,如果 \(\textit{height}[l] < \textit{height}[r]\),移动 \(r\) 指针不会使得结果变得更好,因为容器的高度由较短的那根垂直线决定,所以我们移动 \(l\) 指针。反之,我们移动 \(r\) 指针。
遍历结束后,返回 \(\textit{ans}\) 即可。
时间复杂度 \(O(n)\),其中 \(n\) 是数组 \(\textit{height}\) 的长度。空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def maxArea(self, height: List[int]) -> int:
l, r = 0, len(height) - 1
ans = 0
while l < r:
t = min(height[l], height[r]) * (r - l)
ans = max(ans, t)
if height[l] < height[r]:
l += 1
else:
r -= 1
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution {
public int maxArea(int[] height) {
int l = 0, r = height.length - 1;
int ans = 0;
while (l < r) {
int t = Math.min(height[l], height[r]) * (r - l);
ans = Math.max(ans, t);
if (height[l] < height[r]) {
++l;
} else {
--r;
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public:
int maxArea(vector<int>& height) {
int l = 0, r = height.size() - 1;
int ans = 0;
while (l < r) {
int t = min(height[l], height[r]) * (r - l);
ans = max(ans, t);
if (height[l] < height[r]) {
++l;
} else {
--r;
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13 | func maxArea(height []int) (ans int) {
l, r := 0, len(height)-1
for l < r {
t := min(height[l], height[r]) * (r - l)
ans = max(ans, t)
if height[l] < height[r] {
l++
} else {
r--
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | function maxArea(height: number[]): number {
let [l, r] = [0, height.length - 1];
let ans = 0;
while (l < r) {
const t = Math.min(height[l], height[r]) * (r - l);
ans = Math.max(ans, t);
if (height[l] < height[r]) {
++l;
} else {
--r;
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | impl Solution {
pub fn max_area(height: Vec<i32>) -> i32 {
let mut l = 0;
let mut r = height.len() - 1;
let mut ans = 0;
while l < r {
ans = ans.max(height[l].min(height[r]) * ((r - l) as i32));
if height[l] < height[r] {
l += 1;
} else {
r -= 1;
}
}
ans
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | /**
* @param {number[]} height
* @return {number}
*/
var maxArea = function (height) {
let [l, r] = [0, height.length - 1];
let ans = 0;
while (l < r) {
const t = Math.min(height[l], height[r]) * (r - l);
ans = Math.max(ans, t);
if (height[l] < height[r]) {
++l;
} else {
--r;
}
}
return ans;
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | public class Solution {
public int MaxArea(int[] height) {
int l = 0, r = height.Length - 1;
int ans = 0;
while (l < r) {
int t = Math.Min(height[l], height[r]) * (r - l);
ans = Math.Max(ans, t);
if (height[l] < height[r]) {
++l;
} else {
--r;
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution {
/**
* @param Integer[] $height
* @return Integer
*/
function maxArea($height) {
$l = 0;
$r = count($height) - 1;
$ans = 0;
while ($l < $r) {
$t = min($height[$l], $height[$r]) * ($r - $l);
$ans = max($ans, $t);
if ($height[$l] < $height[$r]) {
++$l;
} else {
--$r;
}
}
return $ans;
}
}
|

