题目描述
给定一个二叉搜索树,请将它的每个 的值替换成树中大于或者等于该 值的所有 值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
示例 1:
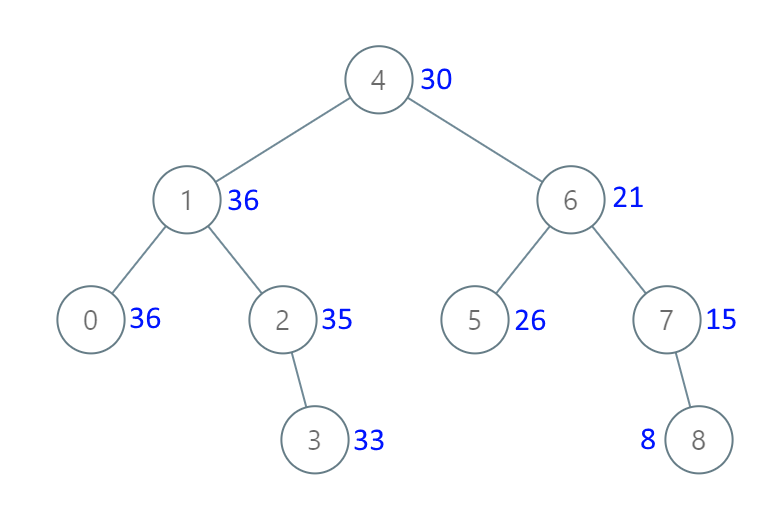
输入: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入: root = [0,null,1]
输出: [1,null,1]
示例 3:
输入: root = [1,0,2]
输出: [3,3,2]
示例 4:
输入: root = [3,2,4,1]
输出: [7,9,4,10]
提示:
树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。
解法
方法一:递归
按照“右根左”的顺序,递归遍历二叉搜索树,累加遍历到的所有节点值到 \(s\) 中,然后每次赋值给对应的 node 节点。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是二叉搜索树的节点数。
Python3 Java C++ Go TypeScript Rust JavaScript Swift
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def convertBST ( self , root : TreeNode ) -> TreeNode :
def dfs ( root ):
nonlocal s
if root is None :
return
dfs ( root . right )
s += root . val
root . val = s
dfs ( root . left )
s = 0
dfs ( root )
return root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int s ;
public TreeNode convertBST ( TreeNode root ) {
dfs ( root );
return root ;
}
private void dfs ( TreeNode root ) {
if ( root == null ) {
return ;
}
dfs ( root . right );
s += root . val ;
root . val = s ;
dfs ( root . left );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
int s = 0 ;
TreeNode * convertBST ( TreeNode * root ) {
dfs ( root );
return root ;
}
void dfs ( TreeNode * root ) {
if ( ! root ) return ;
dfs ( root -> right );
s += root -> val ;
root -> val = s ;
dfs ( root -> left );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func convertBST ( root * TreeNode ) * TreeNode {
s := 0
var dfs func ( * TreeNode )
dfs = func ( root * TreeNode ) {
if root == nil {
return
}
dfs ( root . Right )
s += root . Val
root . Val = s
dfs ( root . Left )
}
dfs ( root )
return root
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function convertBST ( root : TreeNode | null ) : TreeNode | null {
let sum = 0 ;
const dfs = ( root : TreeNode | null ) => {
if ( root == null ) {
return ;
}
dfs ( root . right );
root . val += sum ;
sum = root . val ;
dfs ( root . left );
};
dfs ( root );
return root ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std :: cell :: RefCell ;
use std :: rc :: Rc ;
impl Solution {
fn dfs ( root : & Option < Rc < RefCell < TreeNode >>> , sum : & mut i32 ) {
if let Some ( node ) = root {
Self :: dfs ( & node . borrow (). right , sum );
node . borrow_mut (). val += * sum ;
* sum = node . borrow (). val ;
Self :: dfs ( & node . borrow (). left , sum );
}
}
pub fn convert_bst ( root : Option < Rc < RefCell < TreeNode >>> ) -> Option < Rc < RefCell < TreeNode >>> {
Self :: dfs ( & root , & mut 0 );
root
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 /**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var convertBST = function ( root ) {
let s = 0 ;
function dfs ( root ) {
if ( ! root ) {
return ;
}
dfs ( root . right );
s += root . val ;
root . val = s ;
dfs ( root . left );
}
dfs ( root );
return root ;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 /* class TreeNode {
* var val: Int
* var left: TreeNode?
* var right: TreeNode?
* init() {
* self.val = 0
* self.left = nil
* self.right = nil
* }
* init(_ val: Int) {
* self.val = val
* self.left = nil
* self.right = nil
* }
* init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {
* self.val = val
* self.left = left
* self.right = right
* }
* }
*/
class Solution {
private var s = 0
func convertBST ( _ root : TreeNode ?) -> TreeNode ? {
dfs ( root )
return root
}
private func dfs ( _ root : TreeNode ?) {
guard let node = root else {
return
}
dfs ( node . right )
s += node . val
node . val = s
dfs ( node . left )
}
}
方法二:Morris 遍历
Morris 遍历无需使用栈,时间复杂度 \(O(n)\) ,空间复杂度为 \(O(1)\) 。核心思想是:
定义 s 表示二叉搜索树节点值累加和。遍历二叉树节点:
若当前节点 root 的右子树为空,将当前节点值添加至 s 中,更新当前节点值为 s,并将当前节点更新为 root.left。
若当前节点 root 的右子树不为空,找到右子树的最左节点 next(也即是 root 节点在中序遍历下的后继节点):
若后继节点 next 的左子树为空,将后继节点的左子树指向当前节点 root,并将当前节点更新为 root.right。
若后继节点 next 的左子树不为空,将当前节点值添加 s 中,更新当前节点值为 s,然后将后继节点左子树指向空(即解除 next 与 root 的指向关系),并将当前节点更新为 root.left。
循环以上步骤,直至二叉树节点为空,遍历结束。
最后返回二叉搜索树根节点即可。
Morris 反序中序遍历跟 Morris 中序遍历思路一致,只是将中序遍历的“左根右”变为“右根左”。
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def convertBST ( self , root : TreeNode ) -> TreeNode :
s = 0
node = root
while root :
if root . right is None :
s += root . val
root . val = s
root = root . left
else :
next = root . right
while next . left and next . left != root :
next = next . left
if next . left is None :
next . left = root
root = root . right
else :
s += root . val
root . val = s
next . left = None
root = root . left
return node
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode convertBST ( TreeNode root ) {
int s = 0 ;
TreeNode node = root ;
while ( root != null ) {
if ( root . right == null ) {
s += root . val ;
root . val = s ;
root = root . left ;
} else {
TreeNode next = root . right ;
while ( next . left != null && next . left != root ) {
next = next . left ;
}
if ( next . left == null ) {
next . left = root ;
root = root . right ;
} else {
s += root . val ;
root . val = s ;
next . left = null ;
root = root . left ;
}
}
}
return node ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * convertBST ( TreeNode * root ) {
int s = 0 ;
TreeNode * node = root ;
while ( root ) {
if ( root -> right == nullptr ) {
s += root -> val ;
root -> val = s ;
root = root -> left ;
} else {
TreeNode * next = root -> right ;
while ( next -> left && next -> left != root ) {
next = next -> left ;
}
if ( next -> left == nullptr ) {
next -> left = root ;
root = root -> right ;
} else {
s += root -> val ;
root -> val = s ;
next -> left = nullptr ;
root = root -> left ;
}
}
}
return node ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func convertBST ( root * TreeNode ) * TreeNode {
s := 0
node := root
for root != nil {
if root . Right == nil {
s += root . Val
root . Val = s
root = root . Left
} else {
next := root . Right
for next . Left != nil && next . Left != root {
next = next . Left
}
if next . Left == nil {
next . Left = root
root = root . Right
} else {
s += root . Val
root . Val = s
next . Left = nil
root = root . Left
}
}
}
return node
}