
题目描述
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0 代表空单元格;
- 值
1 代表新鲜橘子;
- 值
2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:
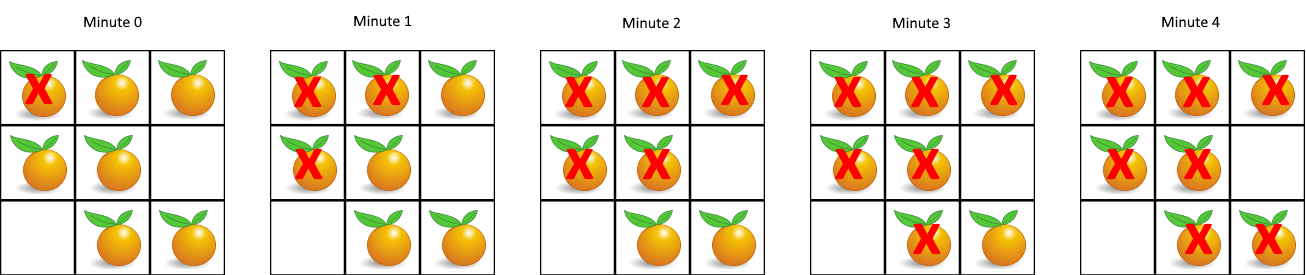
输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个方向上。
示例 3:
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j] 仅为 0、1 或 2
解法
方法一:BFS
我们首先遍历一遍整个网格,统计出新鲜橘子的数量,记为 \(\textit{cnt}\),并且将所有腐烂的橘子的坐标加入队列 \(q\) 中。
接下来,我们进行广度优先搜索,每一轮搜索,我们将队列中的所有腐烂的橘子向四个方向腐烂新鲜橘子,直到队列为空或者新鲜橘子的数量为 \(0\) 为止。
最后,如果新鲜橘子的数量为 \(0\),则返回当前的轮数,否则返回 \(-1\)。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是网格的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution:
def orangesRotting(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
cnt = 0
q = deque()
for i, row in enumerate(grid):
for j, x in enumerate(row):
if x == 2:
q.append((i, j))
elif x == 1:
cnt += 1
ans = 0
dirs = (-1, 0, 1, 0, -1)
while q and cnt:
ans += 1
for _ in range(len(q)):
i, j = q.popleft()
for a, b in pairwise(dirs):
x, y = i + a, j + b
if 0 <= x < m and 0 <= y < n and grid[x][y] == 1:
grid[x][y] = 2
q.append((x, y))
cnt -= 1
if cnt == 0:
return ans
return -1 if cnt else 0
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution {
public int orangesRotting(int[][] grid) {
int m = grid.length, n = grid[0].length;
Deque<int[]> q = new ArrayDeque<>();
int cnt = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
++cnt;
} else if (grid[i][j] == 2) {
q.offer(new int[] {i, j});
}
}
}
final int[] dirs = {-1, 0, 1, 0, -1};
for (int ans = 1; !q.isEmpty() && cnt > 0; ++ans) {
for (int k = q.size(); k > 0; --k) {
var p = q.poll();
for (int d = 0; d < 4; ++d) {
int x = p[0] + dirs[d], y = p[1] + dirs[d + 1];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
grid[x][y] = 2;
q.offer(new int[] {x, y});
if (--cnt == 0) {
return ans;
}
}
}
}
}
return cnt > 0 ? -1 : 0;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
queue<pair<int, int>> q;
int cnt = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
++cnt;
} else if (grid[i][j] == 2) {
q.emplace(i, j);
}
}
}
const int dirs[5] = {-1, 0, 1, 0, -1};
for (int ans = 1; q.size() && cnt; ++ans) {
for (int k = q.size(); k; --k) {
auto [i, j] = q.front();
q.pop();
for (int d = 0; d < 4; ++d) {
int x = i + dirs[d], y = j + dirs[d + 1];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
grid[x][y] = 2;
q.emplace(x, y);
if (--cnt == 0) {
return ans;
}
}
}
}
}
return cnt > 0 ? -1 : 0;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | func orangesRotting(grid [][]int) int {
m, n := len(grid), len(grid[0])
q := [][2]int{}
cnt := 0
for i, row := range grid {
for j, x := range row {
if x == 1 {
cnt++
} else if x == 2 {
q = append(q, [2]int{i, j})
}
}
}
dirs := [5]int{-1, 0, 1, 0, -1}
for ans := 1; len(q) > 0 && cnt > 0; ans++ {
for k := len(q); k > 0; k-- {
p := q[0]
q = q[1:]
for d := 0; d < 4; d++ {
x, y := p[0]+dirs[d], p[1]+dirs[d+1]
if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
grid[x][y] = 2
q = append(q, [2]int{x, y})
if cnt--; cnt == 0 {
return ans
}
}
}
}
}
if cnt > 0 {
return -1
}
return 0
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | function orangesRotting(grid: number[][]): number {
const m: number = grid.length;
const n: number = grid[0].length;
const q: number[][] = [];
let cnt: number = 0;
for (let i: number = 0; i < m; ++i) {
for (let j: number = 0; j < n; ++j) {
if (grid[i][j] === 1) {
cnt++;
} else if (grid[i][j] === 2) {
q.push([i, j]);
}
}
}
const dirs: number[] = [-1, 0, 1, 0, -1];
for (let ans = 1; q.length && cnt; ++ans) {
const t: number[][] = [];
for (const [i, j] of q) {
for (let d = 0; d < 4; ++d) {
const [x, y] = [i + dirs[d], j + dirs[d + 1]];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] === 1) {
grid[x][y] = 2;
t.push([x, y]);
if (--cnt === 0) {
return ans;
}
}
}
}
q.splice(0, q.length, ...t);
}
return cnt > 0 ? -1 : 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | use std::collections::VecDeque;
impl Solution {
pub fn oranges_rotting(mut grid: Vec<Vec<i32>>) -> i32 {
let m = grid.len();
let n = grid[0].len();
let mut q = VecDeque::new();
let mut cnt = 0;
for i in 0..m {
for j in 0..n {
if grid[i][j] == 1 {
cnt += 1;
} else if grid[i][j] == 2 {
q.push_back((i, j));
}
}
}
let dirs = [-1, 0, 1, 0, -1];
for ans in 1.. {
if q.is_empty() || cnt == 0 {
break;
}
let mut size = q.len();
for _ in 0..size {
let (x, y) = q.pop_front().unwrap();
for d in 0..4 {
let nx = x as isize + dirs[d] as isize;
let ny = y as isize + dirs[d + 1] as isize;
if nx >= 0 && nx < m as isize && ny >= 0 && ny < n as isize {
let nx = nx as usize;
let ny = ny as usize;
if grid[nx][ny] == 1 {
grid[nx][ny] = 2;
q.push_back((nx, ny));
cnt -= 1;
if cnt == 0 {
return ans;
}
}
}
}
}
}
if cnt > 0 {
-1
} else {
0
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | /**
* @param {number[][]} grid
* @return {number}
*/
var orangesRotting = function (grid) {
const m = grid.length;
const n = grid[0].length;
let q = [];
let cnt = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 1) {
cnt++;
} else if (grid[i][j] === 2) {
q.push([i, j]);
}
}
}
const dirs = [-1, 0, 1, 0, -1];
for (let ans = 1; q.length && cnt; ++ans) {
let t = [];
for (const [i, j] of q) {
for (let d = 0; d < 4; ++d) {
const x = i + dirs[d];
const y = j + dirs[d + 1];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] === 1) {
grid[x][y] = 2;
t.push([x, y]);
if (--cnt === 0) {
return ans;
}
}
}
}
q = [...t];
}
return cnt > 0 ? -1 : 0;
};
|

