99. 恢复二叉搜索树

题目描述

给你二叉搜索树的根节点 root ，该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。

示例 1：

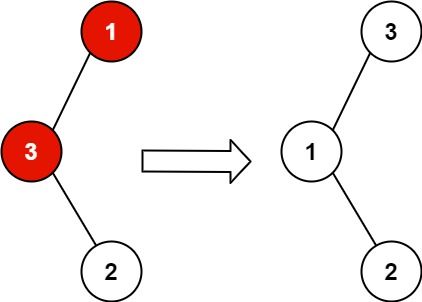
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：

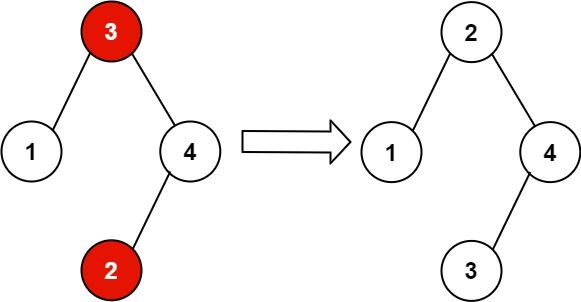
输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

提示：

树上节点的数目在范围 [2, 1000] 内
-2³¹ <= Node.val <= 2³¹ - 1

进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗？

解法

方法一：中序遍历

中序遍历二叉搜索树，得到的序列是递增的。如果有两个节点的值被错误地交换，那么中序遍历得到的序列中，一定会出现两个逆序对。我们用 first 和 second 分别记录这两个逆序对中较小值和较大值的节点，最后交换这两个节点的值即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉搜索树的节点个数。

Python3JavaC++GoJavaScriptC#

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def recoverTree(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """

        def dfs(root):
            if root is None:
                return
            nonlocal prev, first, second
            dfs(root.left)
            if prev and prev.val > root.val:
                if first is None:
                    first = prev
                second = root
            prev = root
            dfs(root.right)

        prev = first = second = None
        dfs(root)
        first.val, second.val = second.val, first.val

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private TreeNode prev;
    private TreeNode first;
    private TreeNode second;

    public void recoverTree(TreeNode root) {
        dfs(root);
        int t = first.val;
        first.val = second.val;
        second.val = t;
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.left);
        if (prev != null && prev.val > root.val) {
            if (first == null) {
                first = prev;
            }
            second = root;
        }
        prev = root;
        dfs(root.right);
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void recoverTree(TreeNode* root) {
        TreeNode* prev = nullptr;
        TreeNode* first = nullptr;
        TreeNode* second = nullptr;
        function<void(TreeNode * root)> dfs = [&](TreeNode* root) {
            if (!root) return;
            dfs(root->left);
            if (prev && prev->val > root->val) {
                if (!first) first = prev;
                second = root;
            }
            prev = root;
            dfs(root->right);
        };
        dfs(root);
        swap(first->val, second->val);
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func recoverTree(root *TreeNode) {
    var prev, first, second *TreeNode
    var dfs func(*TreeNode)
    dfs = func(root *TreeNode) {
        if root == nil {
            return
        }
        dfs(root.Left)
        if prev != nil && prev.Val > root.Val {
            if first == nil {
                first = prev
            }
            second = root
        }
        prev = root
        dfs(root.Right)
    }
    dfs(root)
    first.Val, second.Val = second.Val, first.Val
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var recoverTree = function (root) {
    let prev = null;
    let first = null;
    let second = null;
    function dfs(root) {
        if (!root) {
            return;
        }
        dfs(root.left);
        if (prev && prev.val > root.val) {
            if (!first) {
                first = prev;
            }
            second = root;
        }
        prev = root;
        dfs(root.right);
    }
    dfs(root);
    const t = first.val;
    first.val = second.val;
    second.val = t;
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private TreeNode prev, first, second;

    public void RecoverTree(TreeNode root) {
        dfs(root);
        int t = first.val;
        first.val = second.val;
        second.val = t;
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.left);
        if (prev != null && prev.val > root.val) {
            if (first == null) {
                first = prev;
            }
            second = root;
        }
        prev = root;
        dfs(root.right);
    }
}

99. 恢复二叉搜索树

题目描述

解法

方法一：中序遍历

评论