动态规划
字符串
题目描述
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串 :
s = s1 + s2 + ... + sn t = t1 + t2 + ... + tm |n - m| <= 1交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...
注意: a + b 意味着字符串 a 和 b 连接。
示例 1:
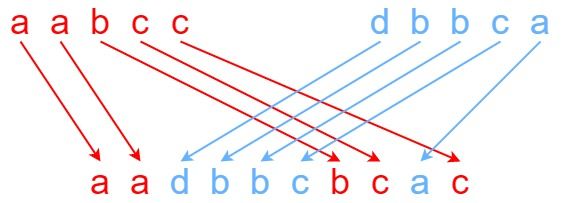
输入: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出: true
示例 2:
输入: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出: false
示例 3:
输入: s1 = "", s2 = "", s3 = ""
输出: true
提示:
0 <= s1.length, s2.length <= 1000 <= s3.length <= 200s1、s2、和 s3 都由小写英文字母组成
进阶: 您能否仅使用 O(s2.length) 额外的内存空间来解决它?
解法
方法一:记忆化搜索
我们记字符串 \(s_1\) 的长度为 \(m\) ,字符串 \(s_2\) 的长度为 \(n\) ,如果 \(m + n \neq |s_3|\) ,那么 \(s_3\) 一定不是 \(s_1\) 和 \(s_2\) 的交错字符串,返回 false。
接下来,我们设计一个函数 \(dfs(i, j)\) ,表示从 \(s_1\) 的第 \(i\) 个字符和 \(s_2\) 的第 \(j\) 个字符开始,能否交错组成 \(s_3\) 的剩余部分。那么答案就是 \(dfs(0, 0)\) 。
函数 \(dfs(i, j)\) 的计算过程如下:
如果 \(i \geq m\) 并且 \(j \geq n\) ,那么说明 \(s_1\) 和 \(s_2\) 都已经遍历完毕,返回 true。
如果 \(i < m\) 并且 \(s_1[i] = s_3[i + j]\) ,那么说明 \(s_1[i]\) 这个字符是 \(s_3[i + j]\) 中的一部分,因此递归地调用 \(dfs(i + 1, j)\) 判断 \(s_1\) 的下一个字符能否和 \(s_2\) 的当前字符匹配,如果能匹配成功,就返回 true。
同理,如果 \(j < n\) 并且 \(s_2[j] = s_3[i + j]\) ,那么说明 \(s_2[j]\) 这个字符是 \(s_3[i + j]\) 中的一部分,因此递归地调用 \(dfs(i, j + 1)\) 判断 \(s_2\) 的下一个字符能否和 \(s_1\) 的当前字符匹配,如果能匹配成功,就返回 true。
否则,返回 false。
为了避免重复计算,我们可以使用记忆化搜索。
时间复杂度 \(O(m \times n)\) ,空间复杂度 \(O(m \times n)\) 。其中 \(m\) 和 \(n\) 分别是字符串 \(s_1\) 和 \(s_2\) 的长度。
Python3 Java C++ Go TypeScript Rust C#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 class Solution :
def isInterleave ( self , s1 : str , s2 : str , s3 : str ) -> bool :
@cache
def dfs ( i : int , j : int ) -> bool :
if i >= m and j >= n :
return True
k = i + j
if i < m and s1 [ i ] == s3 [ k ] and dfs ( i + 1 , j ):
return True
if j < n and s2 [ j ] == s3 [ k ] and dfs ( i , j + 1 ):
return True
return False
m , n = len ( s1 ), len ( s2 )
if m + n != len ( s3 ):
return False
return dfs ( 0 , 0 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 class Solution {
private Map < List < Integer > , Boolean > f = new HashMap <> ();
private String s1 ;
private String s2 ;
private String s3 ;
private int m ;
private int n ;
public boolean isInterleave ( String s1 , String s2 , String s3 ) {
m = s1 . length ();
n = s2 . length ();
if ( m + n != s3 . length ()) {
return false ;
}
this . s1 = s1 ;
this . s2 = s2 ;
this . s3 = s3 ;
return dfs ( 0 , 0 );
}
private boolean dfs ( int i , int j ) {
if ( i >= m && j >= n ) {
return true ;
}
var key = List . of ( i , j );
if ( f . containsKey ( key )) {
return f . get ( key );
}
int k = i + j ;
boolean ans = false ;
if ( i < m && s1 . charAt ( i ) == s3 . charAt ( k ) && dfs ( i + 1 , j )) {
ans = true ;
}
if ( ! ans && j < n && s2 . charAt ( j ) == s3 . charAt ( k ) && dfs ( i , j + 1 )) {
ans = true ;
}
f . put ( key , ans );
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 class Solution {
public :
bool isInterleave ( string s1 , string s2 , string s3 ) {
int m = s1 . size (), n = s2 . size ();
if ( m + n != s3 . size ()) {
return false ;
}
vector < vector < int >> f ( m + 1 , vector < int > ( n + 1 , -1 ));
function < bool ( int , int ) > dfs = [ & ]( int i , int j ) {
if ( i >= m && j >= n ) {
return true ;
}
if ( f [ i ][ j ] != -1 ) {
return f [ i ][ j ] == 1 ;
}
f [ i ][ j ] = 0 ;
int k = i + j ;
if ( i < m && s1 [ i ] == s3 [ k ] && dfs ( i + 1 , j )) {
f [ i ][ j ] = 1 ;
}
if ( ! f [ i ][ j ] && j < n && s2 [ j ] == s3 [ k ] && dfs ( i , j + 1 )) {
f [ i ][ j ] = 1 ;
}
return f [ i ][ j ] == 1 ;
};
return dfs ( 0 , 0 );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 func isInterleave ( s1 string , s2 string , s3 string ) bool {
m , n := len ( s1 ), len ( s2 )
if m + n != len ( s3 ) {
return false
}
f := map [ int ] bool {}
var dfs func ( int , int ) bool
dfs = func ( i , j int ) bool {
if i >= m && j >= n {
return true
}
if v , ok := f [ i * 200 + j ]; ok {
return v
}
k := i + j
f [ i * 200 + j ] = ( i < m && s1 [ i ] == s3 [ k ] && dfs ( i + 1 , j )) || ( j < n && s2 [ j ] == s3 [ k ] && dfs ( i , j + 1 ))
return f [ i * 200 + j ]
}
return dfs ( 0 , 0 )
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 function isInterleave ( s1 : string , s2 : string , s3 : string ) : boolean {
const m = s1 . length ;
const n = s2 . length ;
if ( m + n !== s3 . length ) {
return false ;
}
const f : number [][] = new Array ( m + 1 ). fill ( 0 ). map (() => new Array ( n + 1 ). fill ( 0 ));
const dfs = ( i : number , j : number ) : boolean => {
if ( i >= m && j >= n ) {
return true ;
}
if ( f [ i ][ j ]) {
return f [ i ][ j ] === 1 ;
}
f [ i ][ j ] = - 1 ;
if ( i < m && s1 [ i ] === s3 [ i + j ] && dfs ( i + 1 , j )) {
f [ i ][ j ] = 1 ;
}
if ( f [ i ][ j ] === - 1 && j < n && s2 [ j ] === s3 [ i + j ] && dfs ( i , j + 1 )) {
f [ i ][ j ] = 1 ;
}
return f [ i ][ j ] === 1 ;
};
return dfs ( 0 , 0 );
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64 impl Solution {
#[allow(dead_code)]
pub fn is_interleave ( s1 : String , s2 : String , s3 : String ) -> bool {
let n = s1 . len ();
let m = s2 . len ();
if s1 . len () + s2 . len () != s3 . len () {
return false ;
}
let mut record = vec! [ vec! [ - 1 ; m + 1 ]; n + 1 ];
Self :: dfs (
& mut record ,
n ,
m ,
0 ,
0 ,
& s1 . chars (). collect (),
& s2 . chars (). collect (),
& s3 . chars (). collect (),
)
}
#[allow(dead_code)]
fn dfs (
record : & mut Vec < Vec < i32 >> ,
n : usize ,
m : usize ,
i : usize ,
j : usize ,
s1 : & Vec < char > ,
s2 : & Vec < char > ,
s3 : & Vec < char > ,
) -> bool {
if i >= n && j >= m {
return true ;
}
if record [ i ][ j ] != - 1 {
return record [ i ][ j ] == 1 ;
}
// Set the initial value
record [ i ][ j ] = 0 ;
let k = i + j ;
// Let's try `s1` first
if i < n && s1 [ i ] == s3 [ k ] && Self :: dfs ( record , n , m , i + 1 , j , s1 , s2 , s3 ) {
record [ i ][ j ] = 1 ;
}
// If the first approach does not succeed, let's then try `s2`
if record [ i ][ j ] == 0
&& j < m
&& s2 [ j ] == s3 [ k ]
&& Self :: dfs ( record , n , m , i , j + 1 , s1 , s2 , s3 )
{
record [ i ][ j ] = 1 ;
}
record [ i ][ j ] == 1
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 public class Solution {
private int m ;
private int n ;
private string s1 ;
private string s2 ;
private string s3 ;
private int [,] f ;
public bool IsInterleave ( string s1 , string s2 , string s3 ) {
m = s1 . Length ;
n = s2 . Length ;
if ( m + n != s3 . Length ) {
return false ;
}
this . s1 = s1 ;
this . s2 = s2 ;
this . s3 = s3 ;
f = new int [ m + 1 , n + 1 ];
return dfs ( 0 , 0 );
}
private bool dfs ( int i , int j ) {
if ( i >= m && j >= n ) {
return true ;
}
if ( f [ i , j ] != 0 ) {
return f [ i , j ] == 1 ;
}
f [ i , j ] = - 1 ;
if ( i < m && s1 [ i ] == s3 [ i + j ] && dfs ( i + 1 , j )) {
f [ i , j ] = 1 ;
}
if ( f [ i , j ] == - 1 && j < n && s2 [ j ] == s3 [ i + j ] && dfs ( i , j + 1 )) {
f [ i , j ] = 1 ;
}
return f [ i , j ] == 1 ;
}
}
方法二:动态规划
我们可以将方法一中的记忆化搜索转化为动态规划。
定义 \(f[i][j]\) 表示字符串 \(s_1\) 的前 \(i\) 个字符和字符串 \(s_2\) 的前 \(j\) 个字符是否能交错组成字符串 \(s_3\) 的前 \(i + j\) 个字符。在进行状态转移时,我们可以考虑当前字符是由 \(s_1\) 的最后一个字符还是 \(s_2\) 的最后一个字符得到的,因此有状态转移方程:
\[
f[i][j] = \begin{cases}
f[i - 1][j] & \textit{if } s_1[i - 1] = s_3[i + j - 1] \\
\textit{or } f[i][j - 1] & \textit{if } s_2[j - 1] = s_3[i + j - 1] \\
\textit{false} & \textit{otherwise}
\end{cases}
\]
其中 \(f[0][0] = \textit{true}\) 表示空串是两个空串的交错字符串。
答案即为 \(f[m][n]\) 。
时间复杂度 \(O(m \times n)\) ,空间复杂度 \(O(m \times n)\) 。其中 \(m\) 和 \(n\) 分别是字符串 \(s_1\) 和 \(s_2\) 的长度。
Python3 Java C++ Go TypeScript C#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 class Solution :
def isInterleave ( self , s1 : str , s2 : str , s3 : str ) -> bool :
m , n = len ( s1 ), len ( s2 )
if m + n != len ( s3 ):
return False
f = [[ False ] * ( n + 1 ) for _ in range ( m + 1 )]
f [ 0 ][ 0 ] = True
for i in range ( m + 1 ):
for j in range ( n + 1 ):
k = i + j - 1
if i and s1 [ i - 1 ] == s3 [ k ]:
f [ i ][ j ] = f [ i - 1 ][ j ]
if j and s2 [ j - 1 ] == s3 [ k ]:
f [ i ][ j ] |= f [ i ][ j - 1 ]
return f [ m ][ n ]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution {
public boolean isInterleave ( String s1 , String s2 , String s3 ) {
int m = s1 . length (), n = s2 . length ();
if ( m + n != s3 . length ()) {
return false ;
}
boolean [][] f = new boolean [ m + 1 ][ n + 1 ] ;
f [ 0 ][ 0 ] = true ;
for ( int i = 0 ; i <= m ; ++ i ) {
for ( int j = 0 ; j <= n ; ++ j ) {
int k = i + j - 1 ;
if ( i > 0 && s1 . charAt ( i - 1 ) == s3 . charAt ( k )) {
f [ i ][ j ] = f [ i - 1 ][ j ] ;
}
if ( j > 0 && s2 . charAt ( j - 1 ) == s3 . charAt ( k )) {
f [ i ][ j ] |= f [ i ][ j - 1 ] ;
}
}
}
return f [ m ][ n ] ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 class Solution {
public :
bool isInterleave ( string s1 , string s2 , string s3 ) {
int m = s1 . size (), n = s2 . size ();
if ( m + n != s3 . size ()) {
return false ;
}
bool f [ m + 1 ][ n + 1 ];
memset ( f , false , sizeof ( f ));
f [ 0 ][ 0 ] = true ;
for ( int i = 0 ; i <= m ; ++ i ) {
for ( int j = 0 ; j <= n ; ++ j ) {
int k = i + j - 1 ;
if ( i > 0 && s1 [ i - 1 ] == s3 [ k ]) {
f [ i ][ j ] = f [ i - 1 ][ j ];
}
if ( j > 0 && s2 [ j - 1 ] == s3 [ k ]) {
f [ i ][ j ] |= f [ i ][ j - 1 ];
}
}
}
return f [ m ][ n ];
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 func isInterleave ( s1 string , s2 string , s3 string ) bool {
m , n := len ( s1 ), len ( s2 )
if m + n != len ( s3 ) {
return false
}
f := make ([][] bool , m + 1 )
for i := range f {
f [ i ] = make ([] bool , n + 1 )
}
f [ 0 ][ 0 ] = true
for i := 0 ; i <= m ; i ++ {
for j := 0 ; j <= n ; j ++ {
k := i + j - 1
if i > 0 && s1 [ i - 1 ] == s3 [ k ] {
f [ i ][ j ] = f [ i - 1 ][ j ]
}
if j > 0 && s2 [ j - 1 ] == s3 [ k ] {
f [ i ][ j ] = ( f [ i ][ j ] || f [ i ][ j - 1 ])
}
}
}
return f [ m ][ n ]
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 function isInterleave ( s1 : string , s2 : string , s3 : string ) : boolean {
const m = s1 . length ;
const n = s2 . length ;
if ( m + n !== s3 . length ) {
return false ;
}
const f : boolean [][] = new Array ( m + 1 ). fill ( 0 ). map (() => new Array ( n + 1 ). fill ( false ));
f [ 0 ][ 0 ] = true ;
for ( let i = 0 ; i <= m ; ++ i ) {
for ( let j = 0 ; j <= n ; ++ j ) {
const k = i + j - 1 ;
if ( i > 0 && s1 [ i - 1 ] === s3 [ k ]) {
f [ i ][ j ] = f [ i - 1 ][ j ];
}
if ( j > 0 && s2 [ j - 1 ] === s3 [ k ]) {
f [ i ][ j ] = f [ i ][ j ] || f [ i ][ j - 1 ];
}
}
}
return f [ m ][ n ];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 public class Solution {
public bool IsInterleave ( string s1 , string s2 , string s3 ) {
int m = s1 . Length , n = s2 . Length ;
if ( m + n != s3 . Length ) {
return false ;
}
bool [,] f = new bool [ m + 1 , n + 1 ];
f [ 0 , 0 ] = true ;
for ( int i = 0 ; i <= m ; ++ i ) {
for ( int j = 0 ; j <= n ; ++ j ) {
int k = i + j - 1 ;
if ( i > 0 && s1 [ i - 1 ] == s3 [ k ]) {
f [ i , j ] = f [ i - 1 , j ];
}
if ( j > 0 && s2 [ j - 1 ] == s3 [ k ]) {
f [ i , j ] |= f [ i , j - 1 ];
}
}
}
return f [ m , n ];
}
}
我们注意到,状态 \(f[i][j]\) 只和状态 \(f[i - 1][j]\) 、\(f[i][j - 1]\) 、\(f[i - 1][j - 1]\) 有关,因此我们可以使用滚动数组优化空间复杂度,将空间复杂度优化到 \(O(n)\) 。
Python3 Java C++ Go TypeScript C#
1
2
3
4
5
6
7
8
9
10
11
12
13
14 class Solution :
def isInterleave ( self , s1 : str , s2 : str , s3 : str ) -> bool :
m , n = len ( s1 ), len ( s2 )
if m + n != len ( s3 ):
return False
f = [ True ] + [ False ] * n
for i in range ( m + 1 ):
for j in range ( n + 1 ):
k = i + j - 1
if i :
f [ j ] &= s1 [ i - 1 ] == s3 [ k ]
if j :
f [ j ] |= f [ j - 1 ] and s2 [ j - 1 ] == s3 [ k ]
return f [ n ]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution {
public boolean isInterleave ( String s1 , String s2 , String s3 ) {
int m = s1 . length (), n = s2 . length ();
if ( m + n != s3 . length ()) {
return false ;
}
boolean [] f = new boolean [ n + 1 ] ;
f [ 0 ] = true ;
for ( int i = 0 ; i <= m ; ++ i ) {
for ( int j = 0 ; j <= n ; ++ j ) {
int k = i + j - 1 ;
if ( i > 0 ) {
f [ j ] &= s1 . charAt ( i - 1 ) == s3 . charAt ( k );
}
if ( j > 0 ) {
f [ j ] |= ( f [ j - 1 ] & s2 . charAt ( j - 1 ) == s3 . charAt ( k ));
}
}
}
return f [ n ] ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 class Solution {
public :
bool isInterleave ( string s1 , string s2 , string s3 ) {
int m = s1 . size (), n = s2 . size ();
if ( m + n != s3 . size ()) {
return false ;
}
bool f [ n + 1 ];
memset ( f , false , sizeof ( f ));
f [ 0 ] = true ;
for ( int i = 0 ; i <= m ; ++ i ) {
for ( int j = 0 ; j <= n ; ++ j ) {
int k = i + j - 1 ;
if ( i ) {
f [ j ] &= s1 [ i - 1 ] == s3 [ k ];
}
if ( j ) {
f [ j ] |= ( s2 [ j - 1 ] == s3 [ k ] && f [ j - 1 ]);
}
}
}
return f [ n ];
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 func isInterleave ( s1 string , s2 string , s3 string ) bool {
m , n := len ( s1 ), len ( s2 )
if m + n != len ( s3 ) {
return false
}
f := make ([] bool , n + 1 )
f [ 0 ] = true
for i := 0 ; i <= m ; i ++ {
for j := 0 ; j <= n ; j ++ {
k := i + j - 1
if i > 0 {
f [ j ] = ( f [ j ] && s1 [ i - 1 ] == s3 [ k ])
}
if j > 0 {
f [ j ] = ( f [ j ] || ( s2 [ j - 1 ] == s3 [ k ] && f [ j - 1 ]))
}
}
}
return f [ n ]
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 function isInterleave ( s1 : string , s2 : string , s3 : string ) : boolean {
const m = s1 . length ;
const n = s2 . length ;
if ( m + n !== s3 . length ) {
return false ;
}
const f : boolean [] = new Array ( n + 1 ). fill ( false );
f [ 0 ] = true ;
for ( let i = 0 ; i <= m ; ++ i ) {
for ( let j = 0 ; j <= n ; ++ j ) {
const k = i + j - 1 ;
if ( i ) {
f [ j ] = f [ j ] && s1 [ i - 1 ] === s3 [ k ];
}
if ( j ) {
f [ j ] = f [ j ] || ( f [ j - 1 ] && s2 [ j - 1 ] === s3 [ k ]);
}
}
}
return f [ n ];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 public class Solution {
public bool IsInterleave ( string s1 , string s2 , string s3 ) {
int m = s1 . Length , n = s2 . Length ;
if ( m + n != s3 . Length ) {
return false ;
}
bool [] f = new bool [ n + 1 ];
f [ 0 ] = true ;
for ( int i = 0 ; i <= m ; ++ i ) {
for ( int j = 0 ; j <= n ; ++ j ) {
int k = i + j - 1 ;
if ( i > 0 ) {
f [ j ] &= s1 [ i - 1 ] == s3 [ k ];
}
if ( j > 0 ) {
f [ j ] |= ( f [ j - 1 ] & s2 [ j - 1 ] == s3 [ k ]);
}
}
}
return f [ n ];
}
}