跳转至

96. 不同的二叉搜索树

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

 

示例 1：

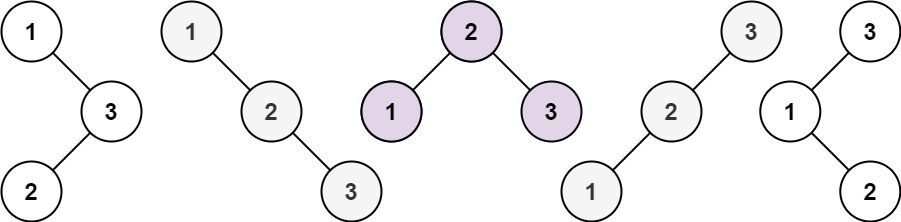
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

 

提示：

  • 1 <= n <= 19

解法

方法一：动态规划

我们定义 $f[i]$ 表示 $[1, i]$ 能产生的二叉搜索树的个数，初始时 $f[0] = 1$，答案为 $f[n]$。

我们可以枚举节点数 $i$，那么左子树节点数 $j \in [0, i - 1]$，右子树节点数 $k = i - j - 1$，左子树节点数和右子树节点数的组合数为 $f[j] \times f[k]$，因此 $f[i] = \sum_{j = 0}^{i - 1} f[j] \times f[i - j - 1]$。

最后返回 $f[n]$ 即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为节点数。

1
2
3
4
5
6
7
class Solution:
    def numTrees(self, n: int) -> int:
        f = [1] + [0] * n
        for i in range(n + 1):
            for j in range(i):
                f[i] += f[j] * f[i - j - 1]
        return f[n]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
    public int numTrees(int n) {
        int[] f = new int[n + 1];
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j < i; ++j) {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        return f[n];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
public:
    int numTrees(int n) {
        vector<int> f(n + 1);
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j < i; ++j) {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        return f[n];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
func numTrees(n int) int {
    f := make([]int, n+1)
    f[0] = 1
    for i := 1; i <= n; i++ {
        for j := 0; j < i; j++ {
            f[i] += f[j] * f[i-j-1]
        }
    }
    return f[n]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function numTrees(n: number): number {
    const f: number[] = Array(n + 1).fill(0);
    f[0] = 1;
    for (let i = 1; i <= n; ++i) {
        for (let j = 0; j < i; ++j) {
            f[i] += f[j] * f[i - j - 1];
        }
    }
    return f[n];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
impl Solution {
    pub fn num_trees(n: i32) -> i32 {
        let n = n as usize;
        let mut f = vec![0; n + 1];
        f[0] = 1;
        for i in 1..=n {
            for j in 0..i {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        f[n] as i32
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
public class Solution {
    public int NumTrees(int n) {
        int[] f = new int[n + 1];
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j < i; ++j) {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        return f[n];
    }
}

评论