
题目描述
在 rows x cols 的网格上,你从单元格 (rStart, cStart) 面朝东面开始。网格的西北角位于第一行第一列,网格的东南角位于最后一行最后一列。
你需要以顺时针按螺旋状行走,访问此网格中的每个位置。每当移动到网格的边界之外时,需要继续在网格之外行走(但稍后可能会返回到网格边界)。
最终,我们到过网格的所有 rows x cols 个空间。
按照访问顺序返回表示网格位置的坐标列表。
示例 1:
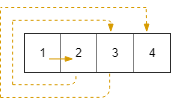
输入:rows = 1, cols = 4, rStart = 0, cStart = 0
输出:[[0,0],[0,1],[0,2],[0,3]]
示例 2:
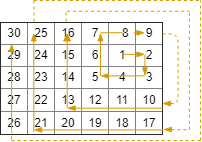
输入:rows = 5, cols = 6, rStart = 1, cStart = 4
输出:[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]
提示:
1 <= rows, cols <= 1000 <= rStart < rows0 <= cStart < cols
解法
方法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | class Solution:
def spiralMatrixIII(
self, rows: int, cols: int, rStart: int, cStart: int
) -> List[List[int]]:
ans = [[rStart, cStart]]
if rows * cols == 1:
return ans
k = 1
while True:
for dr, dc, dk in [[0, 1, k], [1, 0, k], [0, -1, k + 1], [-1, 0, k + 1]]:
for _ in range(dk):
rStart += dr
cStart += dc
if 0 <= rStart < rows and 0 <= cStart < cols:
ans.append([rStart, cStart])
if len(ans) == rows * cols:
return ans
k += 2
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution {
public int[][] spiralMatrixIII(int rows, int cols, int rStart, int cStart) {
int cnt = rows * cols;
int[][] ans = new int[cnt][2];
ans[0] = new int[] {rStart, cStart};
if (cnt == 1) {
return ans;
}
for (int k = 1, idx = 1;; k += 2) {
int[][] dirs = new int[][] {{0, 1, k}, {1, 0, k}, {0, -1, k + 1}, {-1, 0, k + 1}};
for (int[] dir : dirs) {
int r = dir[0], c = dir[1], dk = dir[2];
while (dk-- > 0) {
rStart += r;
cStart += c;
if (rStart >= 0 && rStart < rows && cStart >= 0 && cStart < cols) {
ans[idx++] = new int[] {rStart, cStart};
if (idx == cnt) {
return ans;
}
}
}
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution {
public:
vector<vector<int>> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {
int cnt = rows * cols;
vector<vector<int>> ans;
ans.push_back({rStart, cStart});
if (cnt == 1) return ans;
for (int k = 1;; k += 2) {
vector<vector<int>> dirs = {{0, 1, k}, {1, 0, k}, {0, -1, k + 1}, {-1, 0, k + 1}};
for (auto& dir : dirs) {
int r = dir[0], c = dir[1], dk = dir[2];
while (dk-- > 0) {
rStart += r;
cStart += c;
if (rStart >= 0 && rStart < rows && cStart >= 0 && cStart < cols) {
ans.push_back({rStart, cStart});
if (ans.size() == cnt) return ans;
}
}
}
}
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | func spiralMatrixIII(rows int, cols int, rStart int, cStart int) [][]int {
cnt := rows * cols
ans := [][]int{[]int{rStart, cStart}}
if cnt == 1 {
return ans
}
for k := 1; ; k += 2 {
dirs := [][]int{{0, 1, k}, {1, 0, k}, {0, -1, k + 1}, {-1, 0, k + 1}}
for _, dir := range dirs {
r, c, dk := dir[0], dir[1], dir[2]
for dk > 0 {
rStart += r
cStart += c
if rStart >= 0 && rStart < rows && cStart >= 0 && cStart < cols {
ans = append(ans, []int{rStart, cStart})
if len(ans) == cnt {
return ans
}
}
dk--
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | function spiralMatrixIII(rows: number, cols: number, rStart: number, cStart: number): number[][] {
// prettier-ignore
const dir = [[1,0],[0,1],[-1,0],[0,-1]]
let [x, y, i, size] = [cStart, rStart, 0, 0];
const ans: number[][] = [[y, x]];
const total = rows * cols;
while (ans.length < total) {
if (i % 2 === 0) size++;
for (let j = 0; ans.length < total && j < size; j++) {
x += dir[i][0];
y += dir[i][1];
if (0 <= x && x < cols && 0 <= y && y < rows) {
ans.push([y, x]);
}
}
i = (i + 1) % 4;
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | /**
* @param {number} rows
* @param {number} cols
* @param {number} rStart
* @param {number} cStart
* @return {number[][]}
*/
var spiralMatrixIII = function (rows, cols, rStart, cStart) {
// prettier-ignore
const dir = [[1,0],[0,1],[-1,0],[0,-1]]
let [x, y, i, size] = [cStart, rStart, 0, 0];
const ans = [[y, x]];
const total = rows * cols;
while (ans.length < total) {
if (i % 2 === 0) size++;
for (let j = 0; ans.length < total && j < size; j++) {
x += dir[i][0];
y += dir[i][1];
if (0 <= x && x < cols && 0 <= y && y < rows) {
ans.push([y, x]);
}
}
i = (i + 1) % 4;
}
return ans;
};
|


