
题目描述
给定一个二维网格 grid ,其中:
- '.' 代表一个空房间
- '#' 代表一堵墙
- '@' 是起点
- 小写字母代表钥匙
- 大写字母代表锁
我们从起点开始出发,一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走,也无法穿过一堵墙。如果途经一个钥匙,我们就把它捡起来。除非我们手里有对应的钥匙,否则无法通过锁。
假设 k 为 钥匙/锁 的个数,且满足 1 <= k <= 6,字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之,每个锁有唯一对应的钥匙,每个钥匙也有唯一对应的锁。另外,代表钥匙和锁的字母互为大小写并按字母顺序排列。
返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙,返回 -1 。
示例 1:
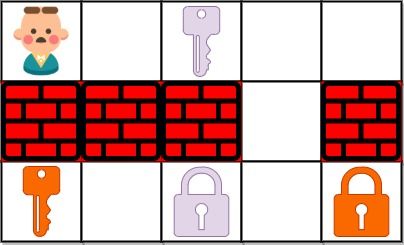
输入:grid = ["@.a..","###.#","b.A.B"]
输出:8
解释:目标是获得所有钥匙,而不是打开所有锁。
示例 2:
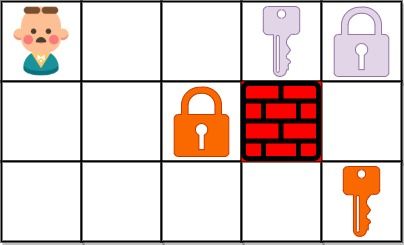
输入:grid = ["@..aA","..B#.","....b"]
输出:6
示例 3:

输入: grid = ["@Aa"]
输出: -1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j] 只含有 '.', '#', '@', 'a'-'f' 以及 'A'-'F'- 钥匙的数目范围是
[1, 6]
- 每个钥匙都对应一个 不同 的字母
- 每个钥匙正好打开一个对应的锁
解法
方法一:状态压缩 + BFS
根据题意,我们需要从起点出发,往上下左右四个方向走,获取所有钥匙,最后返回获取所有钥匙所需要的移动的最少次数。若无法获取所有钥匙,返回 \(-1\)。
首先,我们遍历二维网格,找到起点位置 \((si, sj)\),并统计钥匙的个数 \(k\)。
然后,我们可以使用广度优先搜索 \(BFS\) 来解决本题。由于钥匙的个数范围是 \([1, 6]\),我们可以用一个二进制数来表示钥匙的状态,其中第 \(i\) 位为 \(1\) 表示第 \(i\) 把钥匙已经获取到了,为 \(0\) 表示第 \(i\) 把钥匙还没有获取到。
比如,以下例子中,共有 \(4\) 个二进制位为 \(1\),也就表示有 'b', 'c', 'd', 'f' \(4\) 把钥匙已经获取到了。
1 0 1 1 1 0
^ ^ ^ ^
f d c b
我们定义一个队列 \(q\) 来存储当前位置以及当前拥有的钥匙的状态,即 \((i, j, \textit{state})\),其中 \((i, j)\) 表示当前位置,\(\textit{state}\) 表示当前拥有的钥匙的状态,即 \(\textit{state}\) 的第 \(i\) 位为 \(1\) 表示当前拥有第 \(i\) 把钥匙,否则表示当前没有第 \(i\) 把钥匙。
另外,定义哈希表或数组 \(vis\) 记录当前位置以及当前拥有的钥匙的状态是否已经被访问过,如果访问过,则不需要再次访问。\(vis[i][j][\textit{state}]\) 表示当前位置为 \((i, j)\),当前拥有的钥匙的状态为 \(state\) 时,是否已经被访问过。
我们从起点 \((si, sj)\) 出发,将其加入队列 \(q\),并将 \(vis[si][sj][0]\) 置为 \(true\),表示起点位置以及拥有的钥匙的状态为 \(0\) 时已经被访问过。
在广度优先搜索的过程中,我们每次从队首取出一个位置 \((i, j, \textit{state})\),并判断当前位置是否为终点,即当前位置是否拥有所有的钥匙,即 \(state\) 的二进制表示中的 \(1\) 的个数是否为 \(k\)。如果是,将当前步数作为答案返回。
否则,我们从当前位置出发,往上下左右四个方向走,如果可以走到下一个位置 \((x, y)\),则将 \((x, y, nxt)\) 加入队列 \(q\),其中 \(nxt\) 表示下一个位置的钥匙的状态。
这里 \((x, y)\) 首先需要满足在网格范围内,即 \(0 \leq x < m\) 且 \(0 \leq y < n\)。其次,如果 \((x, y)\) 位置是墙壁,即 grid[x][y] == '#',或者 \((x, y)\) 位置是锁,但我们没有对应的钥匙,即 grid[x][y] >= 'A' && grid[x][y] <= 'F' && (state >> (grid[x][y] - 'A') & 1) == 0),则不能走到位置 \((x, y)\)。否则,我们可以走到位置 \((x, y)\)。
搜索结束,没能找到所有的钥匙,返回 \(-1\)。
时间复杂度 \(O(m\times n\times 2^k)\),空间复杂度 \(O(m\times n\times 2^k)\)。其中 \(m\) 和 \(n\) 分别为网格的行数和列数,而 \(k\) 为钥匙的个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 | class Solution:
def shortestPathAllKeys(self, grid: List[str]) -> int:
m, n = len(grid), len(grid[0])
# 找起点 (si, sj)
si, sj = next((i, j) for i in range(m) for j in range(n) if grid[i][j] == '@')
# 统计钥匙数量
k = sum(v.islower() for row in grid for v in row)
dirs = (-1, 0, 1, 0, -1)
q = deque([(si, sj, 0)])
vis = {(si, sj, 0)}
ans = 0
while q:
for _ in range(len(q)):
i, j, state = q.popleft()
# 找到所有钥匙,返回当前步数
if state == (1 << k) - 1:
return ans
# 往四个方向搜索
for a, b in pairwise(dirs):
x, y = i + a, j + b
nxt = state
# 在边界范围内
if 0 <= x < m and 0 <= y < n:
c = grid[x][y]
# 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if (
c == '#'
or c.isupper()
and (state & (1 << (ord(c) - ord('A')))) == 0
):
continue
# 是钥匙
if c.islower():
# 更新状态
nxt |= 1 << (ord(c) - ord('a'))
# 此状态未访问过,入队
if (x, y, nxt) not in vis:
vis.add((x, y, nxt))
q.append((x, y, nxt))
# 步数加一
ans += 1
return -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64 | class Solution {
private int[] dirs = {-1, 0, 1, 0, -1};
public int shortestPathAllKeys(String[] grid) {
int m = grid.length, n = grid[0].length();
int k = 0;
int si = 0, sj = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
char c = grid[i].charAt(j);
if (Character.isLowerCase(c)) {
// 累加钥匙数量
++k;
} else if (c == '@') {
// 起点
si = i;
sj = j;
}
}
}
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[] {si, sj, 0});
boolean[][][] vis = new boolean[m][n][1 << k];
vis[si][sj][0] = true;
int ans = 0;
while (!q.isEmpty()) {
for (int t = q.size(); t > 0; --t) {
var p = q.poll();
int i = p[0], j = p[1], state = p[2];
// 找到所有钥匙,返回当前步数
if (state == (1 << k) - 1) {
return ans;
}
// 往四个方向搜索
for (int h = 0; h < 4; ++h) {
int x = i + dirs[h], y = j + dirs[h + 1];
// 在边界范围内
if (x >= 0 && x < m && y >= 0 && y < n) {
char c = grid[x].charAt(y);
// 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if (c == '#'
|| (Character.isUpperCase(c) && ((state >> (c - 'A')) & 1) == 0)) {
continue;
}
int nxt = state;
// 是钥匙
if (Character.isLowerCase(c)) {
// 更新状态
nxt |= 1 << (c - 'a');
}
// 此状态未访问过,入队
if (!vis[x][y][nxt]) {
vis[x][y][nxt] = true;
q.offer(new int[] {x, y, nxt});
}
}
}
}
// 步数加一
++ans;
}
return -1;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 | class Solution {
public:
const static inline vector<int> dirs = {-1, 0, 1, 0, -1};
int shortestPathAllKeys(vector<string>& grid) {
int m = grid.size(), n = grid[0].size();
int k = 0;
int si = 0, sj = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
char c = grid[i][j];
// 累加钥匙数量
if (islower(c)) ++k;
// 起点
else if (c == '@')
si = i, sj = j;
}
}
queue<tuple<int, int, int>> q{{{si, sj, 0}}};
vector<vector<vector<bool>>> vis(m, vector<vector<bool>>(n, vector<bool>(1 << k)));
vis[si][sj][0] = true;
int ans = 0;
while (!q.empty()) {
for (int t = q.size(); t; --t) {
auto [i, j, state] = q.front();
q.pop();
// 找到所有钥匙,返回当前步数
if (state == (1 << k) - 1) return ans;
// 往四个方向搜索
for (int h = 0; h < 4; ++h) {
int x = i + dirs[h], y = j + dirs[h + 1];
// 在边界范围内
if (x >= 0 && x < m && y >= 0 && y < n) {
char c = grid[x][y];
// 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if (c == '#' || (isupper(c) && (state >> (c - 'A') & 1) == 0)) continue;
int nxt = state;
// 是钥匙,更新状态
if (islower(c)) nxt |= 1 << (c - 'a');
// 此状态未访问过,入队
if (!vis[x][y][nxt]) {
vis[x][y][nxt] = true;
q.push({x, y, nxt});
}
}
}
}
// 步数加一
++ans;
}
return -1;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 | func shortestPathAllKeys(grid []string) int {
m, n := len(grid), len(grid[0])
var k, si, sj int
for i, row := range grid {
for j, c := range row {
if c >= 'a' && c <= 'z' {
// 累加钥匙数量
k++
} else if c == '@' {
// 起点
si, sj = i, j
}
}
}
type tuple struct{ i, j, state int }
q := []tuple{tuple{si, sj, 0}}
vis := map[tuple]bool{tuple{si, sj, 0}: true}
dirs := []int{-1, 0, 1, 0, -1}
ans := 0
for len(q) > 0 {
for t := len(q); t > 0; t-- {
p := q[0]
q = q[1:]
i, j, state := p.i, p.j, p.state
// 找到所有钥匙,返回当前步数
if state == 1<<k-1 {
return ans
}
// 往四个方向搜索
for h := 0; h < 4; h++ {
x, y := i+dirs[h], j+dirs[h+1]
// 在边界范围内
if x >= 0 && x < m && y >= 0 && y < n {
c := grid[x][y]
// 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if c == '#' || (c >= 'A' && c <= 'Z' && (state>>(c-'A')&1 == 0)) {
continue
}
nxt := state
// 是钥匙,更新状态
if c >= 'a' && c <= 'z' {
nxt |= 1 << (c - 'a')
}
// 此状态未访问过,入队
if !vis[tuple{x, y, nxt}] {
vis[tuple{x, y, nxt}] = true
q = append(q, tuple{x, y, nxt})
}
}
}
}
// 步数加一
ans++
}
return -1
}
|



