跳转至

84. 柱状图中最大的矩形

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

示例 1:

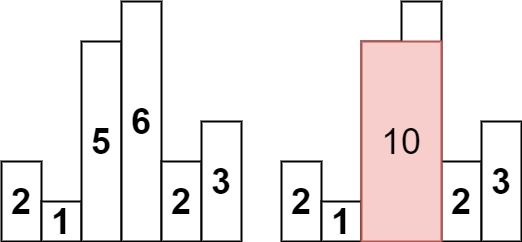
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

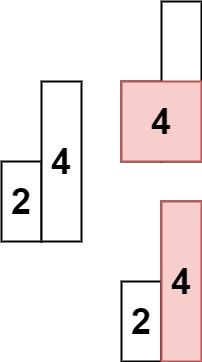
输入： heights = [2,4]
输出： 4

 

提示：

  • 1 <= heights.length <=105
  • 0 <= heights[i] <= 104

解法

方法一：单调栈

我们可以枚举每根柱子的高度 $h$ 作为矩形的高度，利用单调栈，向左右两边找第一个高度小于 $h$ 的下标 $left_i$, $right_i$。那么此时矩形面积为 $h \times (right_i-left_i-1)$，求最大值即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 表示 $heights$ 的长度。

单调栈常见模型：找出每个数左/右边离它最近的且比它大/小的数。模板：

stk = []
for i in range(n):
    while stk and check(stk[-1], i):
        stk.pop()
    stk.append(i)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        stk = []
        left = [-1] * n
        right = [n] * n
        for i, h in enumerate(heights):
            while stk and heights[stk[-1]] >= h:
                right[stk[-1]] = i
                stk.pop()
            if stk:
                left[i] = stk[-1]
            stk.append(i)
        return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = 0, n = heights.length;
        Deque<Integer> stk = new ArrayDeque<>();
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(right, n);
        for (int i = 0; i < n; ++i) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) {
                right[stk.pop()] = i;
            }
            left[i] = stk.isEmpty() ? -1 : stk.peek();
            stk.push(i);
        }
        for (int i = 0; i < n; ++i) {
            res = Math.max(res, heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int res = 0, n = heights.size();
        stack<int> stk;
        vector<int> left(n, -1);
        vector<int> right(n, n);
        for (int i = 0; i < n; ++i) {
            while (!stk.empty() && heights[stk.top()] >= heights[i]) {
                right[stk.top()] = i;
                stk.pop();
            }
            if (!stk.empty()) left[i] = stk.top();
            stk.push(i);
        }
        for (int i = 0; i < n; ++i)
            res = max(res, heights[i] * (right[i] - left[i] - 1));
        return res;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func largestRectangleArea(heights []int) int {
    res, n := 0, len(heights)
    var stk []int
    left, right := make([]int, n), make([]int, n)
    for i := range right {
        right[i] = n
    }
    for i, h := range heights {
        for len(stk) > 0 && heights[stk[len(stk)-1]] >= h {
            right[stk[len(stk)-1]] = i
            stk = stk[:len(stk)-1]
        }
        if len(stk) > 0 {
            left[i] = stk[len(stk)-1]
        } else {
            left[i] = -1
        }
        stk = append(stk, i)
    }
    for i, h := range heights {
        res = max(res, h*(right[i]-left[i]-1))
    }
    return res
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
impl Solution {
    #[allow(dead_code)]
    pub fn largest_rectangle_area(heights: Vec<i32>) -> i32 {
        let n = heights.len();
        let mut left = vec![-1; n];
        let mut right = vec![-1; n];
        let mut stack: Vec<(usize, i32)> = Vec::new();
        let mut ret = -1;

        // Build left vector
        for (i, h) in heights.iter().enumerate() {
            while !stack.is_empty() && stack.last().unwrap().1 >= *h {
                stack.pop();
            }
            if stack.is_empty() {
                left[i] = -1;
            } else {
                left[i] = stack.last().unwrap().0 as i32;
            }
            stack.push((i, *h));
        }

        stack.clear();

        // Build right vector
        for (i, h) in heights.iter().enumerate().rev() {
            while !stack.is_empty() && stack.last().unwrap().1 >= *h {
                stack.pop();
            }
            if stack.is_empty() {
                right[i] = n as i32;
            } else {
                right[i] = stack.last().unwrap().0 as i32;
            }
            stack.push((i, *h));
        }

        // Calculate the max area
        for (i, h) in heights.iter().enumerate() {
            ret = std::cmp::max(ret, (right[i] - left[i] - 1) * *h);
        }

        ret
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using System;
using System.Collections.Generic;
using System.Linq;

public class Solution {
    public int LargestRectangleArea(int[] height) {
        var stack = new Stack<int>();
        var result = 0;
        var i = 0;
        while (i < height.Length || stack.Any())
        {
            if (!stack.Any() || (i < height.Length && height[stack.Peek()] < height[i]))
            {
                stack.Push(i);
                ++i;
            }
            else
            {
                var previousIndex = stack.Pop();
                var area = height[previousIndex] * (stack.Any() ? (i - stack.Peek() - 1) : i);
                result = Math.Max(result, area);
            }
        }

        return result;
    }
}

方法二

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        stk = []
        left = [-1] * n
        right = [n] * n
        for i, h in enumerate(heights):
            while stk and heights[stk[-1]] >= h:
                stk.pop()
            if stk:
                left[i] = stk[-1]
            stk.append(i)
        stk = []
        for i in range(n - 1, -1, -1):
            h = heights[i]
            while stk and heights[stk[-1]] >= h:
                stk.pop()
            if stk:
                right[i] = stk[-1]
            stk.append(i)
        return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))

评论