
题目描述
有一个有 n 个节点的有向图,节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组 graph表示, graph[i]是与节点 i 相邻的节点的整数数组,这意味着从节点 i 到 graph[i]中的每个节点都有一条边。
如果一个节点没有连出的有向边,则该节点是 终端节点 。如果从该节点开始的所有可能路径都通向 终端节点 ,则该节点为 安全节点 。
返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按 升序 排列。
示例 1:
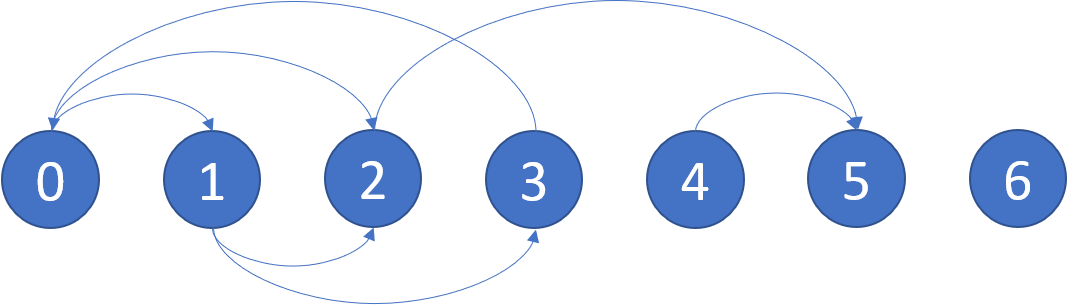
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出:[2,4,5,6]
解释:示意图如上。
节点 5 和节点 6 是终端节点,因为它们都没有出边。
从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6 。
示例 2:
输入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出:[4]
解释:
只有节点 4 是终端节点,从节点 4 开始的所有路径都通向节点 4 。
提示:
n == graph.length1 <= n <= 1040 <= graph[i].length <= n0 <= graph[i][j] <= n - 1graph[i] 按严格递增顺序排列。- 图中可能包含自环。
- 图中边的数目在范围
[1, 4 * 104] 内。
解法
方法一:拓扑排序
出度为零的点是安全的,如果一个点只能到达安全的点,那么它同样是安全的,所以问题转换成了拓扑排序。
我们可以将图中所有边反向,得到一个反图,然后在反图上运行拓扑排序。
时间复杂度 \(O(n+m)\),其中 \(n\) 表示图中的点数,\(m\) 表示图中的边数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution:
def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
rg = defaultdict(list)
indeg = [0] * len(graph)
for i, vs in enumerate(graph):
for j in vs:
rg[j].append(i)
indeg[i] = len(vs)
q = deque([i for i, v in enumerate(indeg) if v == 0])
while q:
i = q.popleft()
for j in rg[i]:
indeg[j] -= 1
if indeg[j] == 0:
q.append(j)
return [i for i, v in enumerate(indeg) if v == 0]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution {
public List<Integer> eventualSafeNodes(int[][] graph) {
int n = graph.length;
int[] indeg = new int[n];
List<Integer>[] rg = new List[n];
Arrays.setAll(rg, k -> new ArrayList<>());
Deque<Integer> q = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
for (int j : graph[i]) {
rg[j].add(i);
}
indeg[i] = graph[i].length;
if (indeg[i] == 0) {
q.offer(i);
}
}
while (!q.isEmpty()) {
int i = q.pollFirst();
for (int j : rg[i]) {
if (--indeg[j] == 0) {
q.offer(j);
}
}
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < n; ++i) {
if (indeg[i] == 0) {
ans.add(i);
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
vector<int> indeg(n);
vector<vector<int>> rg(n);
queue<int> q;
for (int i = 0; i < n; ++i) {
for (int j : graph[i]) rg[j].push_back(i);
indeg[i] = graph[i].size();
if (indeg[i] == 0) q.push(i);
}
while (!q.empty()) {
int i = q.front();
q.pop();
for (int j : rg[i])
if (--indeg[j] == 0) q.push(j);
}
vector<int> ans;
for (int i = 0; i < n; ++i)
if (indeg[i] == 0) ans.push_back(i);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | func eventualSafeNodes(graph [][]int) []int {
n := len(graph)
indeg := make([]int, n)
rg := make([][]int, n)
q := []int{}
for i, vs := range graph {
for _, j := range vs {
rg[j] = append(rg[j], i)
}
indeg[i] = len(vs)
if indeg[i] == 0 {
q = append(q, i)
}
}
for len(q) > 0 {
i := q[0]
q = q[1:]
for _, j := range rg[i] {
indeg[j]--
if indeg[j] == 0 {
q = append(q, j)
}
}
}
ans := []int{}
for i, v := range indeg {
if v == 0 {
ans = append(ans, i)
}
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | /**
* @param {number[][]} graph
* @return {number[]}
*/
var eventualSafeNodes = function (graph) {
const n = graph.length;
const rg = new Array(n).fill(0).map(() => new Array());
const indeg = new Array(n).fill(0);
const q = [];
for (let i = 0; i < n; ++i) {
for (let j of graph[i]) {
rg[j].push(i);
}
indeg[i] = graph[i].length;
if (indeg[i] == 0) {
q.push(i);
}
}
while (q.length) {
const i = q.shift();
for (let j of rg[i]) {
if (--indeg[j] == 0) {
q.push(j);
}
}
}
let ans = [];
for (let i = 0; i < n; ++i) {
if (indeg[i] == 0) {
ans.push(i);
}
}
return ans;
};
|
方法二:DFS + 三色标记法
若起始节点位于一个环内,或者能到达一个环,则该节点不是安全的。否则,该节点是安全的。
- 白色(用 0 表示):该节点尚未被访问;
- 灰色(用 1 表示):该节点位于递归栈中,或者在某个环上;
- 黑色(用 2 表示):该节点搜索完毕,是一个安全节点。

