
题目描述
我们把玻璃杯摆成金字塔的形状,其中 第一层 有 1 个玻璃杯, 第二层 有 2 个,依次类推到第 100 层,每个玻璃杯将盛有香槟。
从顶层的第一个玻璃杯开始倾倒一些香槟,当顶层的杯子满了,任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了,就会等流量的流向它们左右两边的杯子,依次类推。(当最底层的玻璃杯满了,香槟会流到地板上)
例如,在倾倒一杯香槟后,最顶层的玻璃杯满了。倾倒了两杯香槟后,第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后,第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后,第三层中间的玻璃杯盛放了一半的香槟,他两边的玻璃杯各自盛放了四分之一的香槟,如下图所示。
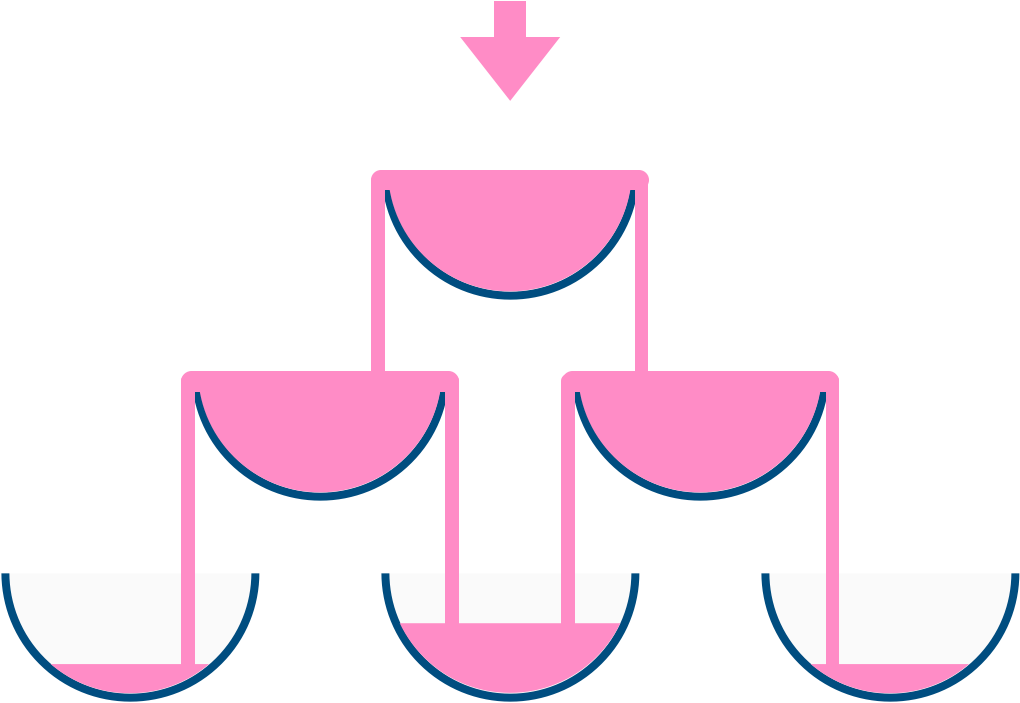
现在当倾倒了非负整数杯香槟后,返回第 i 行 j 个玻璃杯所盛放的香槟占玻璃杯容积的比例( i 和 j 都从0开始)。
示例 1:
输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.00000
解释: 我们在顶层(下标是(0,0))倒了一杯香槟后,没有溢出,因此所有在顶层以下的玻璃杯都是空的。
示例 2:
输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.50000
解释: 我们在顶层(下标是(0,0)倒了两杯香槟后,有一杯量的香槟将从顶层溢出,位于(1,0)的玻璃杯和(1,1)的玻璃杯平分了这一杯香槟,所以每个玻璃杯有一半的香槟。
示例 3:
输入: poured = 100000009, query_row = 33, query_glass = 17
输出: 1.00000
提示:
0 <= poured <= 1090 <= query_glass <= query_row < 100
解法
方法一:模拟
我们直接模拟倒香槟的过程。
定义一个二维数组 \(f\),其中 \(f[i][j]\) 表示第 \(i\) 层第 \(j\) 个玻璃杯中的香槟量。初始时 \(f[0][0] = poured\)。
对于每一层,如果当前杯子的香槟量 \(f[i][j]\) 大于 \(1\),香槟会流向下一层的两个杯子,流入的量为 \(\frac{f[i][j]-1}{2}\),即当前杯子的香槟量减去 \(1\) 后除以 \(2\),然后当前杯子的香槟量更新为 \(1\)。
模拟结束,返回 \(f[query\_row][query\_glass]\) 即可。
由于每一层的香槟量只与上一层的香槟量有关,因此我们可以用滚动数组的方式优化空间复杂度,将二维数组优化为一维数组。
时间复杂度 \(O(n^2)\),空间复杂度 \(O(n)\)。其中 \(n\) 为层数,即 \(query\_row\)。
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:
f = [[0] * 101 for _ in range(101)]
f[0][0] = poured
for i in range(query_row + 1):
for j in range(i + 1):
if f[i][j] > 1:
half = (f[i][j] - 1) / 2
f[i][j] = 1
f[i + 1][j] += half
f[i + 1][j + 1] += half
return f[query_row][query_glass]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public double champagneTower(int poured, int query_row, int query_glass) {
double[][] f = new double[101][101];
f[0][0] = poured;
for (int i = 0; i <= query_row; ++i) {
for (int j = 0; j <= i; ++j) {
if (f[i][j] > 1) {
double half = (f[i][j] - 1) / 2.0;
f[i][j] = 1;
f[i + 1][j] += half;
f[i + 1][j + 1] += half;
}
}
}
return f[query_row][query_glass];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | class Solution {
public:
double champagneTower(int poured, int query_row, int query_glass) {
double f[101][101] = {0.0};
f[0][0] = poured;
for (int i = 0; i <= query_row; ++i) {
for (int j = 0; j <= i; ++j) {
if (f[i][j] > 1) {
double half = (f[i][j] - 1) / 2.0;
f[i][j] = 1;
f[i + 1][j] += half;
f[i + 1][j + 1] += half;
}
}
}
return f[query_row][query_glass];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | func champagneTower(poured int, query_row int, query_glass int) float64 {
f := [101][101]float64{}
f[0][0] = float64(poured)
for i := 0; i <= query_row; i++ {
for j := 0; j <= i; j++ {
if f[i][j] > 1 {
half := (f[i][j] - 1) / 2.0
f[i][j] = 1
f[i+1][j] += half
f[i+1][j+1] += half
}
}
}
return f[query_row][query_glass]
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | function champagneTower(poured: number, query_row: number, query_glass: number): number {
let row = [poured];
for (let i = 1; i <= query_row; i++) {
const nextRow = new Array(i + 1).fill(0);
for (let j = 0; j < i; j++) {
if (row[j] > 1) {
nextRow[j] += (row[j] - 1) / 2;
nextRow[j + 1] += (row[j] - 1) / 2;
}
}
row = nextRow;
}
return Math.min(1, row[query_glass]);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | impl Solution {
pub fn champagne_tower(poured: i32, query_row: i32, query_glass: i32) -> f64 {
let query_row = query_row as usize;
let query_glass = query_glass as usize;
let mut row = vec![poured as f64];
for i in 1..=query_row {
let mut next_row = vec![0f64; i + 1];
for j in 0..i {
if row[j] > 1f64 {
next_row[j] += (row[j] - 1f64) / 2f64;
next_row[j + 1] += (row[j] - 1f64) / 2f64;
}
}
row = next_row;
}
(1f64).min(row[query_glass])
}
}
|
方法二
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:
f = [poured]
for i in range(1, query_row + 1):
g = [0] * (i + 1)
for j, v in enumerate(f):
if v > 1:
half = (v - 1) / 2
g[j] += half
g[j + 1] += half
f = g
return min(1, f[query_glass])
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public double champagneTower(int poured, int query_row, int query_glass) {
double[] f = {poured};
for (int i = 1; i <= query_row; ++i) {
double[] g = new double[i + 1];
for (int j = 0; j < i; ++j) {
if (f[j] > 1) {
double half = (f[j] - 1) / 2.0;
g[j] += half;
g[j + 1] += half;
}
}
f = g;
}
return Math.min(1, f[query_glass]);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution {
public:
double champagneTower(int poured, int query_row, int query_glass) {
double f[101] = {(double) poured};
double g[101];
for (int i = 1; i <= query_row; ++i) {
memset(g, 0, sizeof g);
for (int j = 0; j < i; ++j) {
if (f[j] > 1) {
double half = (f[j] - 1) / 2.0;
g[j] += half;
g[j + 1] += half;
}
}
memcpy(f, g, sizeof g);
}
return min(1.0, f[query_glass]);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | func champagneTower(poured int, query_row int, query_glass int) float64 {
f := []float64{float64(poured)}
for i := 1; i <= query_row; i++ {
g := make([]float64, i+1)
for j, v := range f {
if v > 1 {
half := (v - 1) / 2.0
g[j] += half
g[j+1] += half
}
}
f = g
}
return math.Min(1, f[query_glass])
}
|

