797. 所有可能的路径

题目描述

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

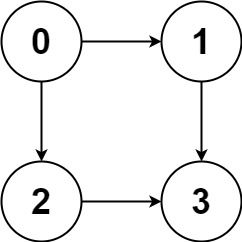
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

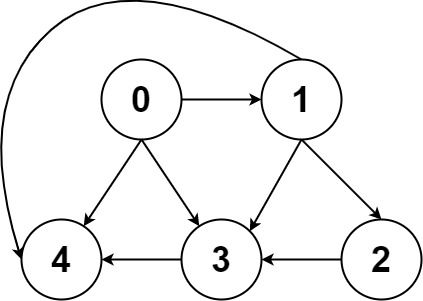
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素 互不相同
保证输入为 有向无环图（DAG）

解法

方法一

Python3JavaC++GoRustJavaScriptTypeScript

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        n = len(graph)
        q = deque([[0]])
        ans = []
        while q:
            path = q.popleft()
            u = path[-1]
            if u == n - 1:
                ans.append(path)
                continue
            for v in graph[u]:
                q.append(path + [v])
        return ans

class Solution {
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        int n = graph.length;
        Queue<List<Integer>> queue = new ArrayDeque<>();
        queue.offer(Arrays.asList(0));
        List<List<Integer>> ans = new ArrayList<>();
        while (!queue.isEmpty()) {
            List<Integer> path = queue.poll();
            int u = path.get(path.size() - 1);
            if (u == n - 1) {
                ans.add(path);
                continue;
            }
            for (int v : graph[u]) {
                List<Integer> next = new ArrayList<>(path);
                next.add(v);
                queue.offer(next);
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<vector<int>> graph;
    vector<vector<int>> ans;

    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        this->graph = graph;
        vector<int> path;
        path.push_back(0);
        dfs(0, path);
        return ans;
    }

    void dfs(int i, vector<int> path) {
        if (i == graph.size() - 1) {
            ans.push_back(path);
            return;
        }
        for (int j : graph[i]) {
            path.push_back(j);
            dfs(j, path);
            path.pop_back();
        }
    }
};

func allPathsSourceTarget(graph [][]int) [][]int {
    var path []int
    path = append(path, 0)
    var ans [][]int

    var dfs func(i int)
    dfs = func(i int) {
        if i == len(graph)-1 {
            ans = append(ans, append([]int(nil), path...))
            return
        }
        for _, j := range graph[i] {
            path = append(path, j)
            dfs(j)
            path = path[:len(path)-1]
        }
    }

    dfs(0)
    return ans
}

impl Solution {
    fn dfs(i: usize, path: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, graph: &Vec<Vec<i32>>) {
        path.push(i as i32);
        if i == graph.len() - 1 {
            res.push(path.clone());
        }
        for j in graph[i].iter() {
            Self::dfs(*j as usize, path, res, graph);
        }
        path.pop();
    }

    pub fn all_paths_source_target(graph: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let mut res = Vec::new();
        Self::dfs(0, &mut vec![], &mut res, &graph);
        res
    }
}

/**
 * @param {number[][]} graph
 * @return {number[][]}
 */
var allPathsSourceTarget = function (graph) {
    const ans = [];
    const t = [0];

    const dfs = t => {
        const cur = t[t.length - 1];
        if (cur == graph.length - 1) {
            ans.push([...t]);
            return;
        }
        for (const v of graph[cur]) {
            t.push(v);
            dfs(t);
            t.pop();
        }
    };

    dfs(t);
    return ans;
};

function allPathsSourceTarget(graph: number[][]): number[][] {
    const ans: number[][] = [];

    const dfs = (path: number[]) => {
        const curr = path.at(-1)!;
        if (curr === graph.length - 1) {
            ans.push([...path]);
            return;
        }

        for (const v of graph[curr]) {
            path.push(v);
            dfs(path);
            path.pop();
        }
    };

    dfs([0]);

    return ans;
}

方法二

Python3Java

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        def dfs(t):
            if t[-1] == len(graph) - 1:
                ans.append(t[:])
                return
            for v in graph[t[-1]]:
                t.append(v)
                dfs(t)
                t.pop()

        ans = []
        dfs([0])
        return ans

class Solution {
    private List<List<Integer>> ans;
    private int[][] graph;

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        ans = new ArrayList<>();
        this.graph = graph;
        List<Integer> t = new ArrayList<>();
        t.add(0);
        dfs(t);
        return ans;
    }

    private void dfs(List<Integer> t) {
        int cur = t.get(t.size() - 1);
        if (cur == graph.length - 1) {
            ans.add(new ArrayList<>(t));
            return;
        }
        for (int v : graph[cur]) {
            t.add(v);
            dfs(t);
            t.remove(t.size() - 1);
        }
    }
}

797. 所有可能的路径

题目描述

解法

方法一

方法二

评论