790. 多米诺和托米诺平铺

题目描述

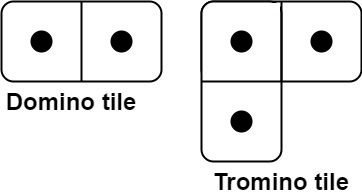
有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 10⁹ + 7 取模的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

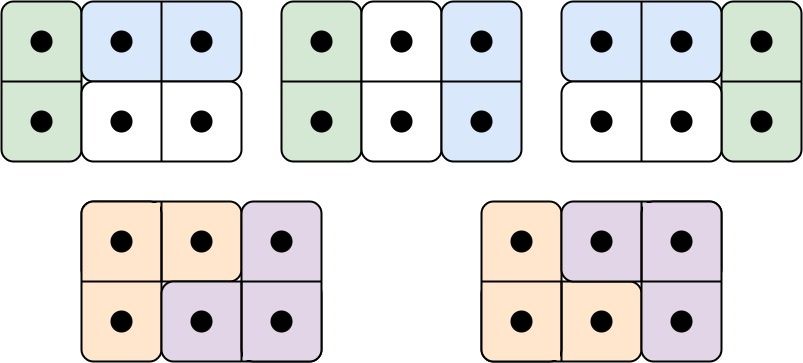
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2:

输入: n = 1
输出: 1

提示：

1 <= n <= 1000

解法

方法一：动态规划

我们首先要读懂题意，题目实际上是让我们求铺满 \(2\times n\) 的面板的方案数，其中面板上的每个正方形只能被一个瓷砖覆盖。

瓷砖的形状有两种，分别是 2 x 1 型和 L 型，并且两种瓷砖都可以旋转。我们将旋转后的瓷砖分别记为 1 x 2 型和 L' 型。

我们定义 \(f[i][j]\) 表示平铺前 \(2\times i\) 的面板，其中 \(j\) 表示最后一列的状态。最后一列有 \(4\) 种状态，分别是：

最后一列铺满，记为 \(0\)
最后一列只铺了上方一个瓷砖，记为 \(1\)
最后一列只铺了下方一个瓷砖，记为 \(2\)
最后一列没有铺瓷砖，记为 \(3\)

那么答案就是 \(f[n][0]\)。初始时 \(f[0][0]=1\)，其余 \(f[0][j]=0\)。

我们考虑铺到第 \(i\) 列，来看看状态转移方程：

当 \(j=0\) 时，最后一列铺满，可由前一列的 \(0,1,2,3\) 四种状态铺上对应的瓷砖转移而来，即 \(f[i-1][0]\) 铺上 1 x 2 型瓷砖，或者 \(f[i-1][1]\) 铺上 L' 型瓷砖，或者 \(f[i-1][2]\) 铺上 L' 型瓷砖，或者 \(f[i-1][3]\) 铺上两块 2 x 1 型瓷砖。因此 \(f[i][0]=\sum_{j=0}^3f[i-1][j]\)。

当 \(j=1\) 时，最后一列只铺了上方一个瓷砖，可由前一列的 \(2,3\) 两种状态转移而来，即 \(f[i-1][2]\) 铺上 2 x 1 型瓷砖，或者 \(f[i-1][3]\) 铺上 L 型瓷砖。因此 \(f[i][1]=f[i-1][2]+f[i-1][3]\)。

当 \(j=2\) 时，最后一列只铺了下方一个瓷砖，可由前一列的 \(1,3\) 两种状态转移而来，即 \(f[i-1][1]\) 铺上 2 x 1 型瓷砖，或者 \(f[i-1][3]\) 铺上 L' 型瓷砖。因此 \(f[i][2]=f[i-1][1]+f[i-1][3]\)。

当 \(j=3\) 时，最后一列没有铺瓷砖，可由前一列的 \(0\) 一种状态转移而来。因此 \(f[i][3]=f[i-1][0]\)。

可以发现，状态转移方程中只涉及到前一列的状态，因此我们可以使用滚动数组优化空间复杂度。

注意，过程中的状态数值可能会很大，因此需要对 \(10^9+7\) 取模。

时间复杂度 \(O(n)\)，空间复杂度 \(O(1)\)。其中 \(n\) 为面板的列数。

Python3JavaC++Go

class Solution:
    def numTilings(self, n: int) -> int:
        @cache
        def dfs(i, j):
            if i > n or j > n:
                return 0
            if i == n and j == n:
                return 1
            ans = 0
            if i == j:
                ans = (
                    dfs(i + 2, j + 2)
                    + dfs(i + 1, j + 1)
                    + dfs(i + 2, j + 1)
                    + dfs(i + 1, j + 2)
                )
            elif i > j:
                ans = dfs(i, j + 2) + dfs(i + 1, j + 2)
            else:
                ans = dfs(i + 2, j) + dfs(i + 2, j + 1)
            return ans % mod

        mod = 10**9 + 7
        return dfs(0, 0)

class Solution {
    public int numTilings(int n) {
        long[] f = {1, 0, 0, 0};
        int mod = (int) 1e9 + 7;
        for (int i = 1; i <= n; ++i) {
            long[] g = new long[4];
            g[0] = (f[0] + f[1] + f[2] + f[3]) % mod;
            g[1] = (f[2] + f[3]) % mod;
            g[2] = (f[1] + f[3]) % mod;
            g[3] = f[0];
            f = g;
        }
        return (int) f[0];
    }
}

class Solution {
public:
    const int mod = 1e9 + 7;

    int numTilings(int n) {
        long f[4] = {1, 0, 0, 0};
        for (int i = 1; i <= n; ++i) {
            long g[4] = {0, 0, 0, 0};
            g[0] = (f[0] + f[1] + f[2] + f[3]) % mod;
            g[1] = (f[2] + f[3]) % mod;
            g[2] = (f[1] + f[3]) % mod;
            g[3] = f[0];
            memcpy(f, g, sizeof(g));
        }
        return f[0];
    }
};

func numTilings(n int) int {
    f := [4]int{}
    f[0] = 1
    const mod int = 1e9 + 7
    for i := 1; i <= n; i++ {
        g := [4]int{}
        g[0] = (f[0] + f[1] + f[2] + f[3]) % mod
        g[1] = (f[2] + f[3]) % mod
        g[2] = (f[1] + f[3]) % mod
        g[3] = f[0]
        f = g
    }
    return f[0]
}

方法二

Python3

class Solution:
    def numTilings(self, n: int) -> int:
        f = [1, 0, 0, 0]
        mod = 10**9 + 7
        for i in range(1, n + 1):
            g = [0] * 4
            g[0] = (f[0] + f[1] + f[2] + f[3]) % mod
            g[1] = (f[2] + f[3]) % mod
            g[2] = (f[1] + f[3]) % mod
            g[3] = f[0]
            f = g
        return f[0]

790. 多米诺和托米诺平铺

题目描述

解法

方法一：动态规划

方法二

评论