766. 托普利茨矩阵
题目描述
给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵,返回 true ;否则,返回 false 。
如果矩阵上每一条由左上到右下的对角线上的元素都相同,那么这个矩阵是 托普利茨矩阵 。
示例 1:
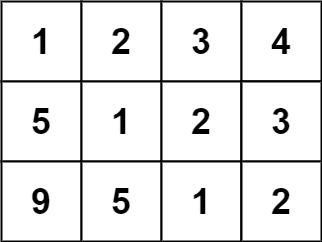
输入:matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]] 输出:true 解释: 在上述矩阵中, 其对角线为: "[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。 各条对角线上的所有元素均相同, 因此答案是 True 。
示例 2:
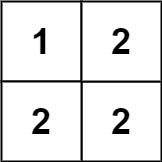
输入:matrix = [[1,2],[2,2]] 输出:false 解释: 对角线 "[1, 2]" 上的元素不同。
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200 <= matrix[i][j] <= 99
进阶:
- 如果矩阵存储在磁盘上,并且内存有限,以至于一次最多只能将矩阵的一行加载到内存中,该怎么办?
- 如果矩阵太大,以至于一次只能将不完整的一行加载到内存中,该怎么办?
解法
方法一:一次遍历
遍历矩阵,若出现元素与其左上角的元素不等的情况,返回 false。否则,遍历结束后返回 true。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(1)\)。其中 \(m\) 和 \(n\) 分别为矩阵的行数和列数。
1 2 3 4 5 6 7 8 | |
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | |
1 2 3 4 5 6 7 8 9 10 11 | |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | |